Index

1. Electrical Circuit Elements
2. Voltage and Current Sources
3. Kirchhoff's Laws
4. Important Pre-requisites before understanding the kirchhoff's laws
5. Kirchhoff's Current law (KCL)
6. Kirchhoff's Voltage Law (KVL)
7. Sign Convention for KVL
8. A better example to understand both KCL and KVL
9. Example 2 (KCL and KVL)
10. Example 3 (KCL and KVL)
11. Superposition, Thevenin and Norton's Theorems
12. Superposition Theorem
13. Example (Superposition Theorem)
14. Thevenin's Theorem
15. Norton's Theorem
16. Relationship between Thevenin and Norton
17. Example (Thevenin and Norton's Theorem)
18. 🧭 DC Circuit Analysis — Reasoning Traces & Concept Map (Important summary to keep in mind for DC circuit's theorem and circuit analysis)

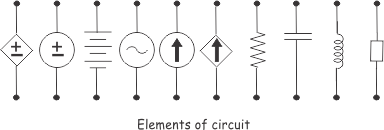
Electrical Circuit Elements

What is an Electric Circuit?

An electric circuit is an interconnection of circuit elements forming a closed path for electric current to flow. A circuit element is the most basic building block that cannot be subdivided further and is characterized completely by its voltage-current relationship.

The Three Passive Elements

There are three fundamental passive circuit elements: Resistor (R), Inductor (L), and Capacitor (C). These are called "passive" because they do not generate electrical energy—they either dissipate it or store it.

1. Resistor (R)

What it does: A resistor introduces electrical friction or resistance in the path of electric current.

Physical behavior: It opposes the flow of current and converts electrical energy into heat—similar to how friction in mechanics dissipates kinetic energy.

2. Inductor (L)

What it does: An inductor is a coil of wire that stores energy in a magnetic field when current flows through it.

Physical behavior: It resists changes in current—think of it like inertia in mechanics, where mass resists changes in velocity.

Voltage-Current Relationship:

$V=L\frac{dI}{dt}$

where $L$ is inductance (in Henries $H$) and $\frac{dI}{dt}$ is the rate of change of current.

Key characteristic: An inductor offers little opposition to steady DC current but strongly opposes AC current or any changing current. The energy stored in an inductor is: $E=\frac{1}{2}L{I}^2$, analogous to kinetic energy $\frac{1}{2}m{v}^2$

3. Capacitor (C)

What it does: A capacitor stores electrical energy in an electric field between two conducting plates.

Physical behavior: It resists changes in voltage—like a spring storing potential energy when compressed.

Voltage-Current Relationship:

$I=C\frac{dV}{dt}$

or equivalently: $Q=CV$

where $C$ is the capacitance (in Farads F), $Q$ is charge (in Coulombs) and $V$ is voltage.

Key characteristic: A capacitor blocks DC current once fully charged but allows AC current to pass. The energy stored is: $E=\frac{1}{2}C{V}^2$, similar to elastic potential energy in a spring.

Voltage and Current Sources

https://www.geeksforgeeks.org/electrical-engineering/what-is-voltage-source/#independent-voltage-sources

These are the active elements that provide electrical energy to circuits, unlike passive elements (R, L, C) that either dissipate or store energy.

Types of Sources

Sources are classified into two main categories:

1. Independent Sources - their output doesn't depend on other circuit variables​.

2. Dependent Sources - their output is controlled by another voltage or current in the circuit.

Independent Voltage Source

An independent voltage source maintains a constant voltage across it's terminals, regardless of the current drawn from it. Think of it as a "voltage enforcer".

Now, under voltage sources, there are two main types of voltage sources:

Ideal Voltage Source

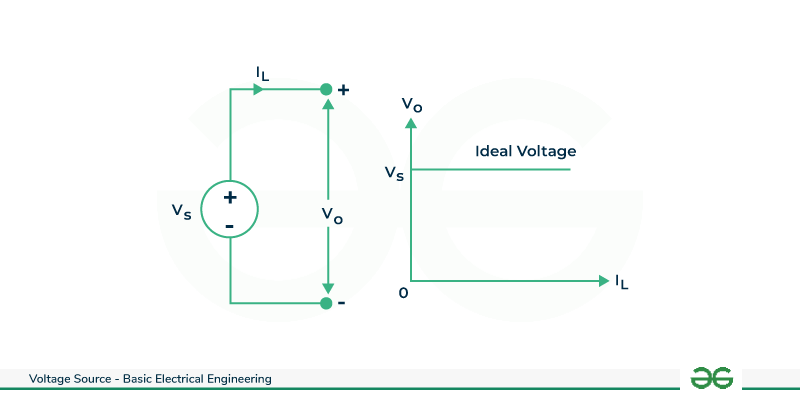
Characteristics:

• Supplies constant voltage regardless of load current​
• Has zero internal resistance ($R_s=0$)​
• Terminal voltage always equals source voltage (no voltage drop)​
• Can theoretically supply infinite current
• 100% efficient (no power loss)

Practical Voltage Source

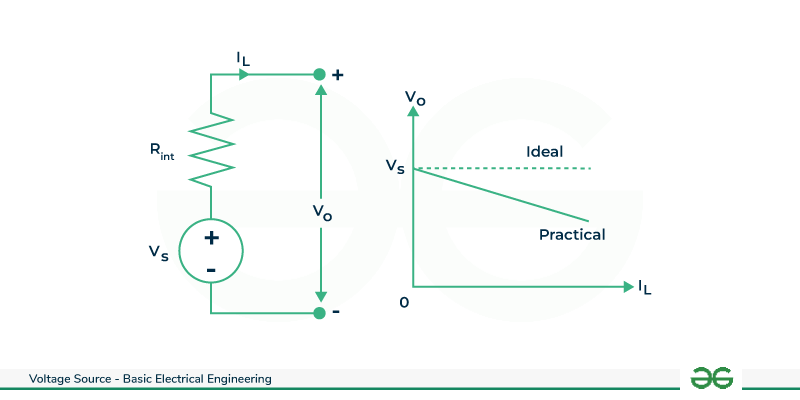
Characteristics:

• Has a small internal resistance ($R_s$) in series.
• Terminal voltage drops as current increases: $V_{\text{terminal}}=V_{\text{source}}-I{R}_s$
• More realistic representation of real batteries and generators.

Direct Voltage Source

Devices or components in electrical circuits that produce a constant voltage output and maintain a constant potential difference across their terminals are referred to as direct voltage sources or direct current (DC) sources.

Output at a Constant Voltage

• Characteristic: The essential element of an immediate voltage source is its capacity to supply a consistent voltage level over the long run.
• Stability: This security is significant in applications where a steady electrical potential is required.

Unidirectional Current Flow

• Flow of Charge: Electric charge (current) flows in a single direction in a direct voltage source. The negative terminal is replaced by the positive terminal by electrons.

• Straightforward Circuitry: This effortlessness of the current stream makes DC sources appropriate for direct circuit plans.

Alternating Voltage Sources

Alternating Voltage Sources, regularly referred to as Alternating Current (AC) sources, are gadgets or components in electrical circuits that produce a consistently changing voltage yield. AC sources, in contrast to Direct Current (DC) sources, produce a sinusoidal voltage that changes over time.

Sinusoidal Voltage Variation

• Characteristic: The characterizing element of AC sources is the sinusoidal variety of voltage over the long run. This indicates that the voltage fluctuates between positive and negative values regularly.

• Representation: The voltage waveform is frequently represented mathematically by a sine or cosine function.

Polarity Reversal

• Polarity Change: The electric current in AC sources occasionally reverses direction. Electrons move to and froth, making a substituting stream.

• Frequency: Hertz (Hz) is the unit of measurement for the rate at which the polarity shifts.

Common Types of Alternating Voltage Sources

• Generators: Electromagnetic induction results in the production of alternating voltage by AC generators, such as those found in power plants.

• Power Outlets: AC voltage is typically provided by household power outlets. AC at 60 Hz is the norm in many places.

Dependent Voltage Sources

A dependent voltage source is a type of voltage source whose output voltage is dependent on any other voltage or current in the circuit. Controlled voltage sources are two other names for dependent voltage sources.

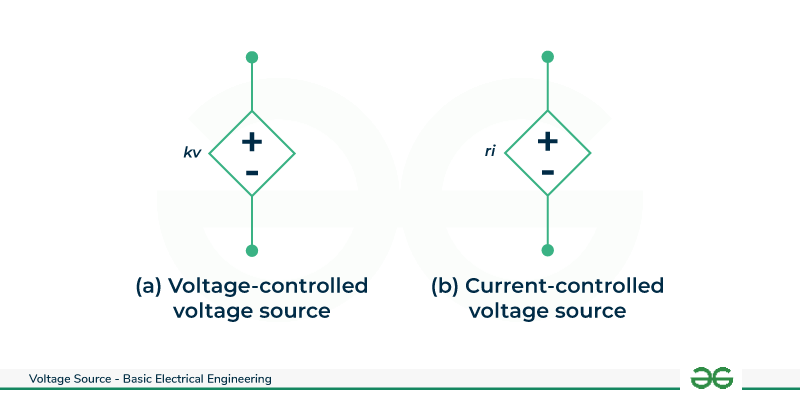
There are two types of controlled voltage sources:

• Voltage Controlled Voltage Source (VCVS) / Voltage Dependent Voltage Source (VDVS)
• Current Controlled Voltage Source (CCVS) / Current Dependent Voltage Source (CDVS)

Voltage-dependent Voltage Source

A voltage-dependent voltage source (VDVS) or voltage-controlled voltage source (VCVS) is a voltage source whose output voltage is dependent on the voltage in any other part of the electric circuit.

Current Controlled Voltage Source

n contrast, a voltage source is referred to as a current-dependent voltage source (CDVS) or a current-controlled voltage source (CCVS) when its output voltage is dependent on the current in any other part of the circuit.

Kirchhoff's Laws

Important Pre-requisites before understanding the kirchhoff's laws

https://www.electrical4u.com/nodes-branches-and-loops-of-a-circuit/

1. Branch

A branch is a single circuit element (like a resistor, voltage source, or capacitor) connecting two points, or any path containing a single element. Think of it as a "road segment" in our circuit.

Any circuit element connects between two nodes in the circuit. The path from one node to another through this element is called a branch of the circuit.

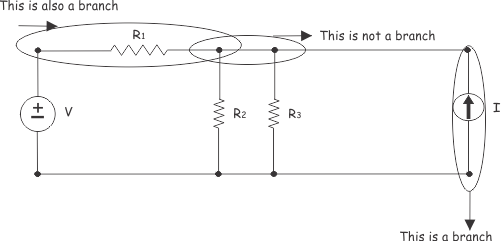
2. Node

A node is a junction point where two or more branches meet.

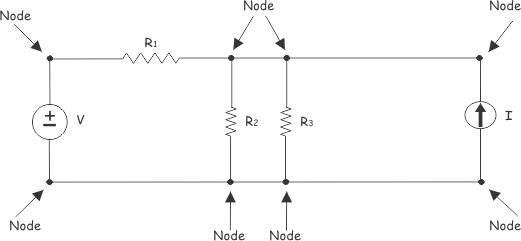
If three is no element between two or more connected adjacent nodes, these nodes can be recombined as a single node.

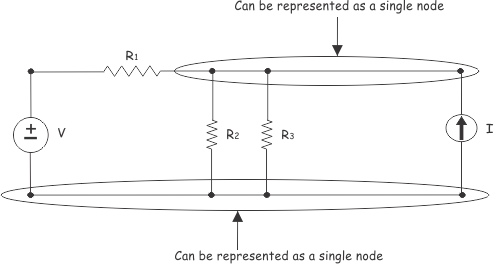
which can be re-drawn as:

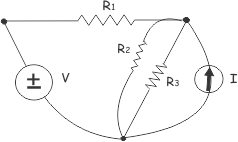
3. Loop

A loop is any closed path in a circuit that starts and ends at the same node without crossing any node twice. Like tracing a circle around your circuit.

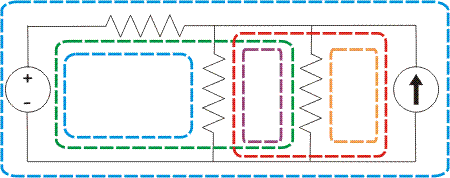
Series vs Parallel Circuits

These two configurations determine how current and voltage behave in your circuit.

Series Circuit

Definition: Components are connected end-to-end in a single path, forming one continuous loop.

Key Characteristics

• Current behavior: The same current flows through all components. Think of water flowing through a single pipe—the flow rate is identical everywhere.

  $I_{total}=I_1=I_2=I_3$

• Voltage behaviour: =The source voltage is divided (shared) among the components=. Each component gets a portion of the total voltage.

  $V_{total}=V_1+V_2+V_3+\cdots$

• Resistance: Total resistance is the sum of individual resistances.

  $R_{eq}=R_1+R_2+R_3+\cdots +R_n$

Critical weakness: If one component fails, the entire circuit breaks—like old Christmas lights.

Parallel Circuit

Definition: Components are connected across common points with multiple paths for current.

Key Characteristics

• Voltage behaviour: The same voltage appears across all components. Each component connects directly to the source voltage.

  $V_{total}=V_1=V_2=V_3$

• Current behavior: The source current splits at junctions and divides among the branches. The sum of branch currents equals the total current.

  $I_{total}=I_1+I_2+I_3$

• Resistance: Total resistance decreases and is less than the smallest individual resistance. More paths mean easier current flow.

  $\frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\cdots +\frac{1}{R_n}$

Quick Comparison Table

Why This Matters for Kirchhoff's Laws

Now here's the connection: Kirchhoff's Laws mathematically describe what we just discussed:​

• KCL (Kirchhoff's Current Law) explains how current behaves at nodes (especially relevant for parallel circuits)​

• KVL (Kirchhoff's Voltage Law) explains how voltage behaves around loops (especially relevant for series circuits)

Ohm's Law

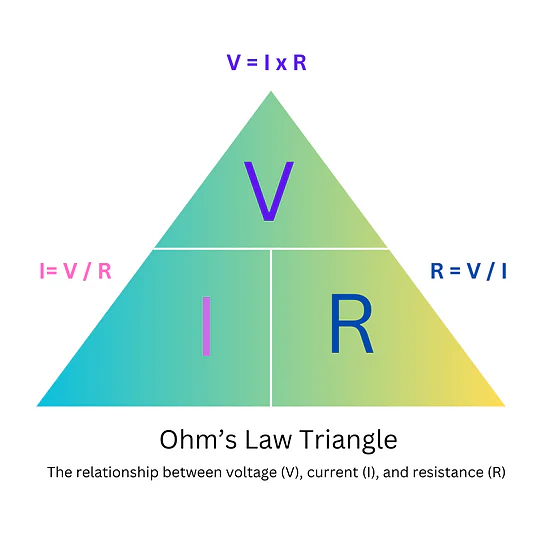
Ohm's Law describes the relationship between voltage, current, and resistance in an electrical circuit, stating that current is directly proportional to voltage and inversely proportional to resistance, as long as physical conditions like temperature remain constant.

The law is primarily expressed with the formula:

or in other forms as the image above shows.

Kirchhoff's Current law (KCL)

Also known as Kirchhoff's First Law or the Junction Rule.

The Law Statement

"The algebraic sum of all currents entering and exiting a node must equal zero".

Or equivalently: "The total current entering a junction equals the total current leaving that junction".

Mathematical Expression

or written another way:

Why is the sum zero?

We’re saying:

“If we give every branch current a sign based on our direction convention, their algebraic sum must equal zero.”

In other words:

• Outgoing currents get a $+$

• Incoming currents get a $–$

• The total signed sum = $0$

where you treat currents entering as positive and currents leaving as negative (or vice versa—just be consistent).

Physical Basis

KCL is based on the Law of Conservation of Charge. A node is just a connection point—it cannot create, destroy, or accumulate charge. Therefore, whatever charge flows in must flow out.

Think of it like water at a pipe junction: the amount of water flowing in equals the amount flowing out (assuming no leaks or storage).

Simple Example

Consider a node with 5 branches: currents $I_1$ and $I_2$ entering, currents $I_3$, $I_4$ and $I_5$ leaving.

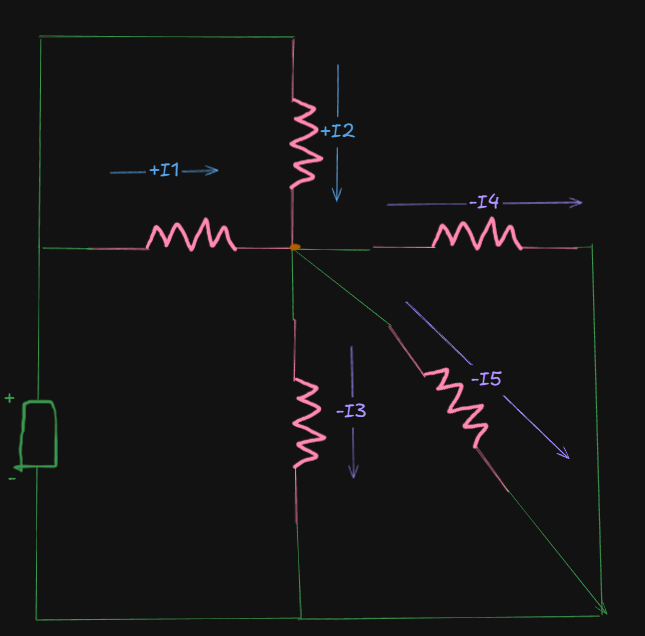
Well here is this odd looking circuit here, that has two incoming branches and 3 outgoing branches, all from a single node.

Applying KCL (entering currents = positive, leaving currents = negative)

Rearranging, we get:

This confirms: total current in = total current out.

When to use KCL

Apply KCL at nodes (junctions) where you need to find unknown currents, especially useful for analyzing parallel circuits.

Kirchhoff's Voltage Law (KVL)

Also known as Kirchhoff's Second Law or the Loop Rule.

The Law Statement

"The algebraic sum of all voltage differences around any closed loop is zero".

Or equivalently: "The sum of voltage rises equals the sum of voltage drops around a closed loop".

Mathematical Expression

$\sum V=0$

around any closed loop.

Physical Basis

KVL is based on the Law of Conservation of Energy. When you traverse a complete loop and return to your starting point, you must be at the same electrical potential—you can't gain or lose net energy going in a circle.

Sign Convention for KVL

This is crucial! When traversing a loop:

Voltage Sources:

• Moving from - to + terminal: counts as positive (voltage rise)

• Moving from + to - terminal: counts as negative(voltage drop)

Resistors/passive elements:

• Moving against current direction (- to +): positive (voltage rise)

• Moving with current direction (+ to -): negative (voltage drop)

Simple Example

Consider a loop with a voltage source $V_s$ and three resistors $R_1$, $R_2$, $R_3$ in series.

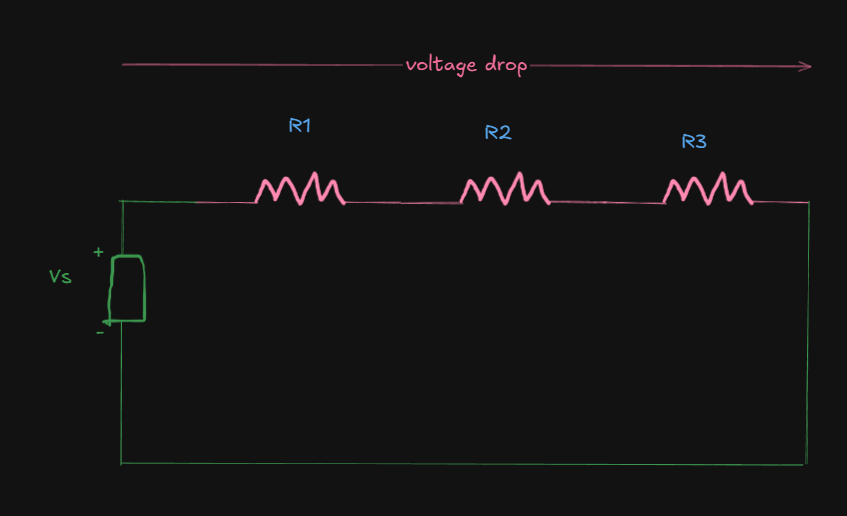
Applying KVL clockwise:

$+V_s-V_{R_1}-V_{R_2}-V_{R_3}=0$

So, the net voltage remains zero.

Now, if we apply ohm's law here ($V=IR$)

We get:

$+V_s=V_{R_1}+V_{R_2}+V_{R_3}$

$+V_s=I{R}_1+I{R}_2+I{R}_3$

$V_s=I(R_1+R_2+R_3)$

This shows how source voltage divides across resistors in series.

When to use KVL

Apply KVL around loops when you need to find unknown voltages or relate voltages in a circuit, especially useful for analyzing series circuits.

A better example to understand both KCL and KVL

(Also falls under the topic of Analysis of Simple DC circuits)

https://www.youtube.com/watch?v=2Zu3ppq3n8I (KCL, KVL and Ohm's law)

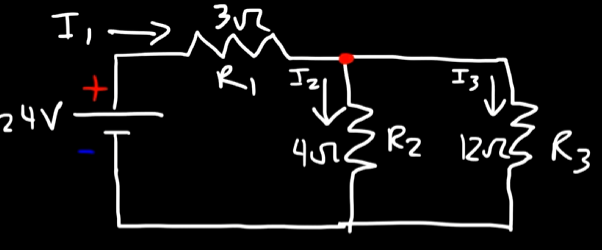
Say we have this circuit here.

And we are tasked to find out the currents $I_1$, $I_2$ and $I_3$

So, first, we have to analyze the voltage flow using the loop rule of Kirchhoff.

We know that:

• Moving from - to + terminal: counts as positive (voltage rise)

• Moving from + to - terminal: counts as negative(voltage drop)

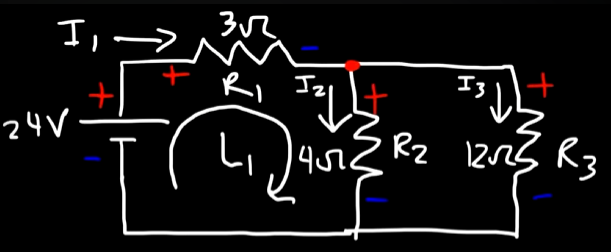
So, by analyzing the circuit as a whole, we see that current $I_1$ enters the red highlighted node and then splits into two branches $I_2$ and $I_3$.

From that current split, using KCL, we can get this equation:

So in this loop $L_1$, since we are following the direction of current i.e. going from the positive to the negative terminal, we will experience a voltage drop (due to the electric potential drop as it moves from a higher to a lower potential).

So, for both the resistors involved in the loop $L_1$, going clockwise.

From KVL, the sum of all voltages in a circuit loop must equal to zero.

So,

That's equation 2.

Now, from the second loop:

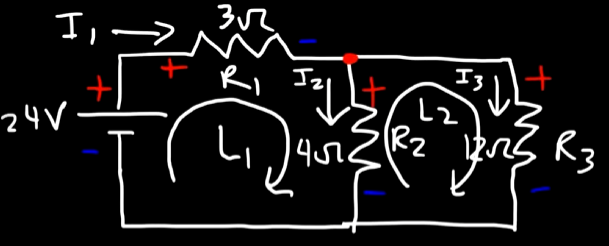
The current will start flowing from $R_3$ first then get back to $R_2$.

So, for $R_3$, the current goes from positive to negative terminals, i.e. causing a voltage drop.

So, we have: $-12I_3$.

For $R_2$, the current goes from a negative to positive terminal, causing a voltage increase.

So, we have: $+4I_2$.

Using KVL, we get:

So, in total, we got 3 equations:

Now it's just plain linear algebra from here on out.

So, by solving these equations we get:

$I_1=4$ A, $I_2=3$A, $I_3=1A$.

Example 2

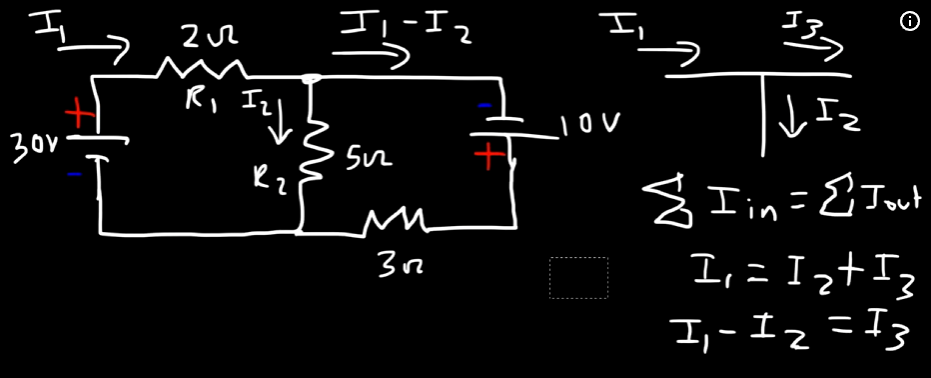
So, we have another circuit, however this time it has two voltage sources.

We will, similarly make loops and analyze the circuits to find out the current flowing through each of the resistors $R_1$, $R_2$ and $R_3$.

The part that you see in the picture that the leaving current from the node that's supposed to be $I_3$ being written as $I_1-I_2$ instead is just simplification for calculation purposes.

That comes from the equation:

$I_1=I_2+I_3$, by KCL.

Which is then rearranged to be:

$I_3=I_1-I_2$.

Anyways, so in loop 1.

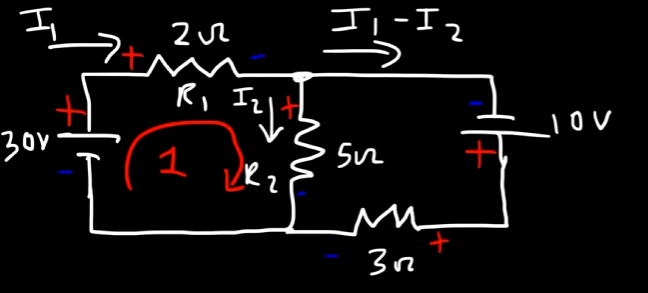
We have the voltage source: $+30$ V.
For resistor $R_1$, we have voltage drop, so that's : $-2I_1$.
For resistor $R_2$, another voltage drop, so that's: $-5I_2$.

By KVL, we have our equation:

or:

Next, for loop 2:

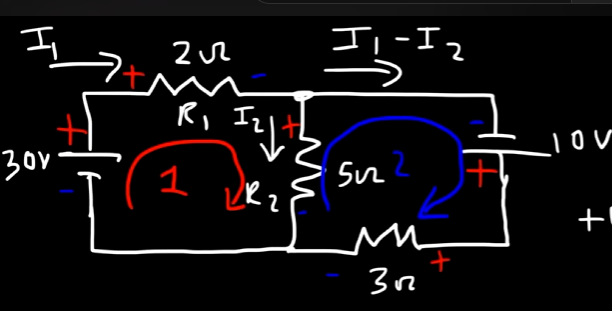
We have the secondary voltage source: $+10$ V.

The voltage current flows from $R_3$, then to $R_2$.

For, $R_3$, we have a voltage drop again, thus: $-3I_3$.

Or: $-3(I_1-I_2)$.

Next, for $R_2$, there is a voltage lift (voltage increase), since the current flows from the negative to the positive terminal:

Thus,: $5I_2$.

So, by KVL, we have our second equation:

or:

or:

Now, we have all our equations:

Now, getting the current values is a matter of simple linear algebra.

By solving the equations, we get the three current values as:

$I_1=9.355$ A, $I_2=2.258$ A, $I_3=I_1-I_2=7.097A$.

Now, further on, if we were to find out the exact voltage drops per resistor, we can easily do so now, by applying ohm's law per resistor with their current values.

So, for $R_1$, the voltage drop is:

$V_1=2\times 9.355=18.71$ V

For $R_2$, the voltage drop is:

$V_2=5\times 2.258=11.29$ V (Also verifiable if you just do $30-18.71=11.29$ V, since that's the residual voltage after leaving $R_1$.)

For $R_3$, the voltage drop is:

$V_3=3\times 7.097=21.291$ V.

Example 3

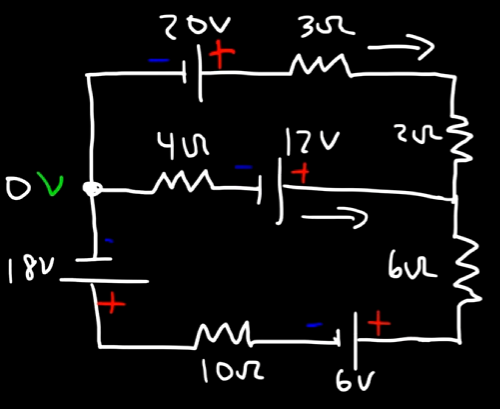
Now, we have to deal with this scary looking circuit.

Starting with loop 1.

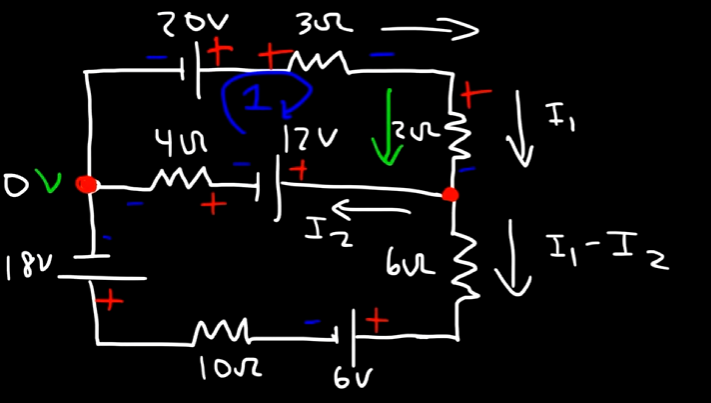
We have a clockwise loop.

For the $3\mathrm{\Omega }$ resistor, $R_1$, we have a voltage drop.

So, that's $-3I_1$.

Now, the $2\mathrm{\Omega }$ resistor $R_2$, it will share the same current $I_1$, due to being in a series connection with $R_1$.

Thus, $-2I_1$.

Now, when the $I_1$ current reaches the splitting node, it branches off into two currents $I_2$, going down the 12V source line and $I_3$ going straight down to the $6\mathrm{\Omega }$ resistor.

So, by KCL, we get an equation:

$I_1=I_2+I_3$.

Or,

$\boxed{{\displaystyle I_3=I_1-I_2}}$.

Focusing on loop 1 only, for the 12V source, the current goes from the positive to negative terminals, continuing the voltage drop.

So we have this down as $-12$ V.

Next for the $4\mathrm{\Omega }$ resistor, it's yet again a voltage drop.

So, that will be $-4I_2$.

So, for the loop 1, by KVL, we have the equation as:

or:

Next up we have loop 2:

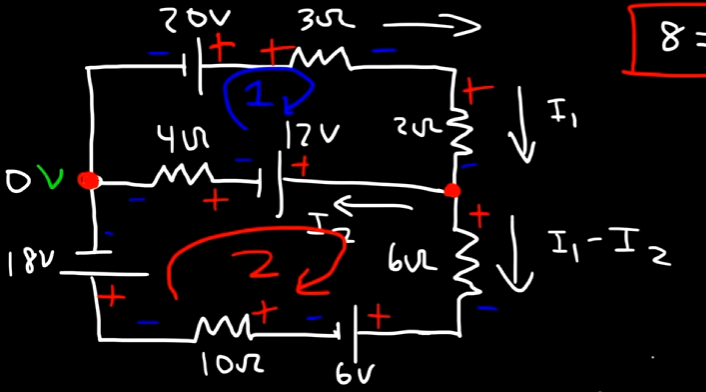
Starting from the 12V source:

$+12$ V.

For the $6\mathrm{\Omega }$ resistor it's a voltage drop, so: $-6(I_1-I_2)$.

Then comes the 6V source having a voltage drop as well.

Then comes the $10\mathrm{\Omega }$ resistor which again has a voltage drop, so that's $-10(I_1-I_2)$, since the $10\mathrm{\Omega }$ resistor in series with the $6\mathrm{\Omega }$ resistor.

Then comes the 18V source with a voltage drop as well.

Lastly at the end of the loop comes the $4\mathrm{\Omega }$ resistor with a voltage lift. So that's: $4I_2$.

So, the equation for this loop will be:

or:

or:

So, we now have the three equations:

Getting the current values from here on out is a simple matter of linear algebra.

Thus, by solving the equations, we can get the current values as:

$I_1=0.6829$ A
$I_2=1.1464$ A

Now, we have encountered a fundamental problem.

$I_1$ is less than $I_2$. So following the current equation for $I_3$ would result in a negative current value, which is impossible in real life.

Thus our initial assumption that $I_1-I_2=I_3$ is wrong, this means that the current was not flowing downwards from the $2\mathrm{\Omega }$ to the $6\mathrm{\Omega }$ resistor as we thought, but it's the reverse, the current is flowing upwards from the $6\mathrm{\Omega }$ resistor to the $2\mathrm{\Omega }$ resistor.

The current split at the junction is fundamentally the same, but the true direction of flow is the reverse of what we assumed.

So, $I_3=I_2-I_1$.

Now that's going to give us a positive current value of $0.4635$ A.

Now, you must be thinking, so how do I know how to make the correct assumption while predicting the flow of current?

The short answer: You don't. You make an assumption, then follow through with the math, and the math provides the verification you need to check which direction the current was flowing per branch (source or resistor) of the circuit.

The corrected signs accordingly are:

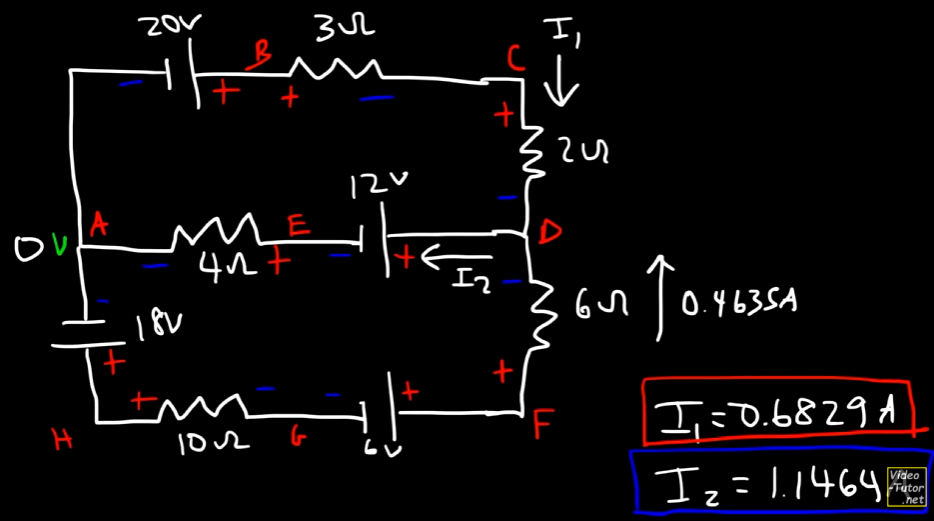
You can see that the terminals for the lower half of the circuit, for loop 2, have been reversed to match the flow accordingly, specifically the $6\mathrm{\Omega }$ resistor, whose signs now match the flow of current through it.

Now that we have all the current values, calculating the voltage at each junction would be easier if we just followed ohm's law per resistor and then proceeded with subtraction and addition as per the voltage drops/lifts as it is in the circuit.

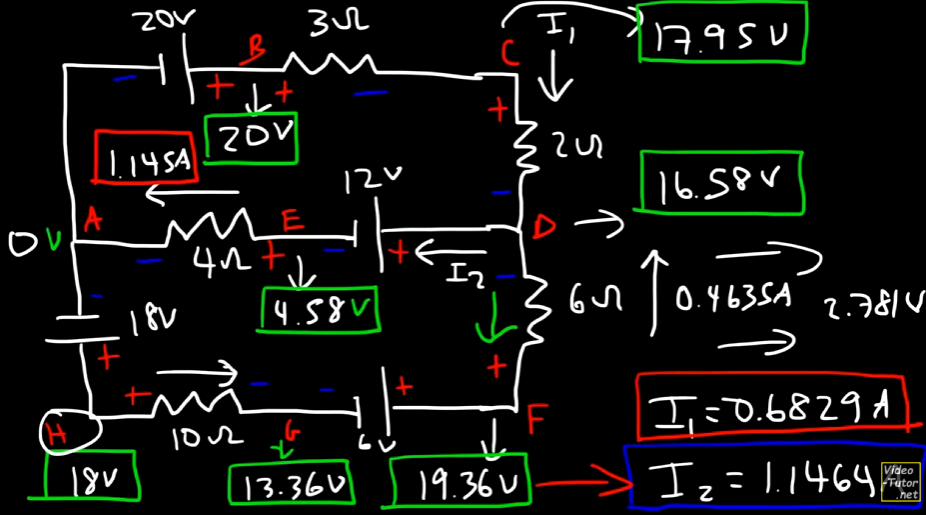
There is one more example in the video, but since these 3 examples would more than suffice to cement the understanding of KCL, KVL and analysis of DC circuits, the last one is left open-ended for the reader's understanding.

Superposition, Thevenin and Norton's Theorems

Superposition Theorem

https://www.youtube.com/watch?v=EX52BuZxpQM

The Superposition Theorem states that in a linear circuit with multiple independent sources (voltage or current), the total current or voltage at any point is the algebraic sum of the currents or voltages produced by each source acting alone.

Physical Principle

This theorem exploits the linearity of circuit elements—meaning the response is directly proportional to the input. It breaks a complex multi-source problem into simpler single-source problems.

How to Apply Superposition Theorem

Follow these systematic steps:

Step 1: Choose one independent source to keep "active"​

Step 2: "Turn off" all other independent sources:​

• Replace voltage sources with a short circuit (0V)​
• Replace current sources with an open circuit (0A)​
• Keep all resistors in place​

Step 3: Analyze the simplified circuit using Ohm's Law, KVL, KCL, or other methods to find the contribution of that one source​

Step 4: Repeat Steps 1-3 for each independent source in the circuit​

Step 5: Add algebraically all the individual contributions (considering signs/directions) to get the total current or voltage

Example

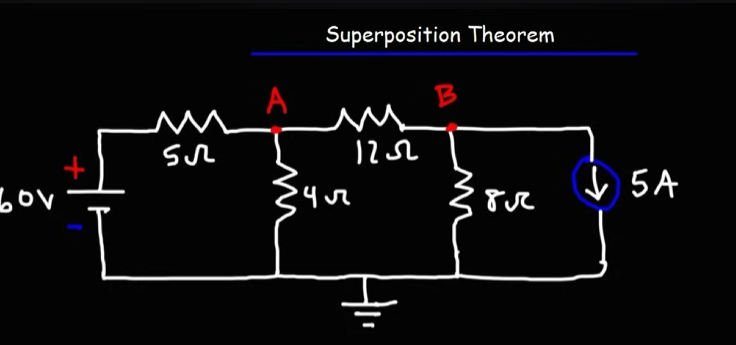
Let's take this circuit for an example.

To find out all the current values per resistors, voltage on the nodes we have to find out the values per source individually, then add them up in the end.

First Half

So, for the 60V source. Notice that the $5A$ source has been replaced with an open circuit.

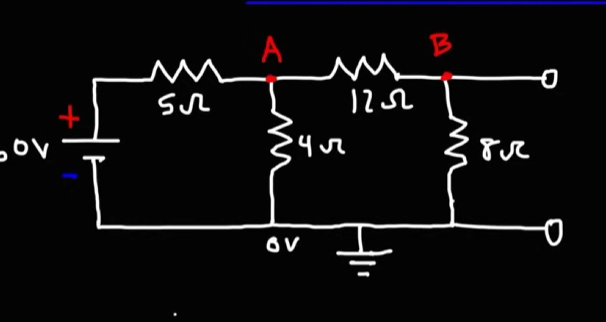
Using KCL, let's say the current going into the $5\mathrm{\Omega }$ resistor branches off at node A into two currents $I_2$ going into the $4\mathrm{\Omega }$ resistor and $I_3$ going to the $12\mathrm{\Omega }$ resistor.

By KCL: $I_1=I_2+I_3$ or $I_3=I_1-I_2$.

For loop 1: assuming the flow of current to be in a clockwise loop,

for the $5\mathrm{\Omega }$ resistor that's $-5I_1$.
for the $4\mathrm{\Omega }$ resistor that's $-4I_2$.

So, by KVL, we get the equation as:

For loop 2:

For the $12\mathrm{\Omega }$ resistor that's $-12(I_1-I_2)$
For the $8\mathrm{\Omega }$ resistor that's again $-8(I_1-I_2)$ (series connection(check the ends of the resistors, where they connect to), so it gets the same current).

For the $4\mathrm{\Omega }$ resistor, that's a voltage lift, so it's going to be $4I_2$.

The equation becomes:

or:

From equation 1:

Applying this in equation 2:

Substituting $I_2$ back:

Now, $I_3=I_1-I_2=1.2A$

The voltage drop at the $5\mathrm{\Omega }$ resistor would be:

So, the voltage at node A would be:

Voltage drop at the $12\mathrm{\Omega }$ resistor would be:

Thus the voltage at node $B$ would be:

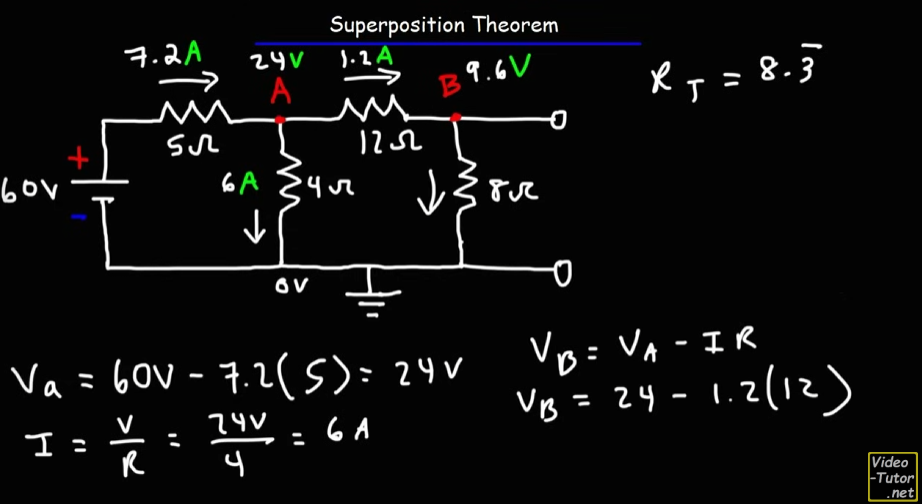
And that matches what we did, although the person in the video took a much simpler approach than I did.

Second Half

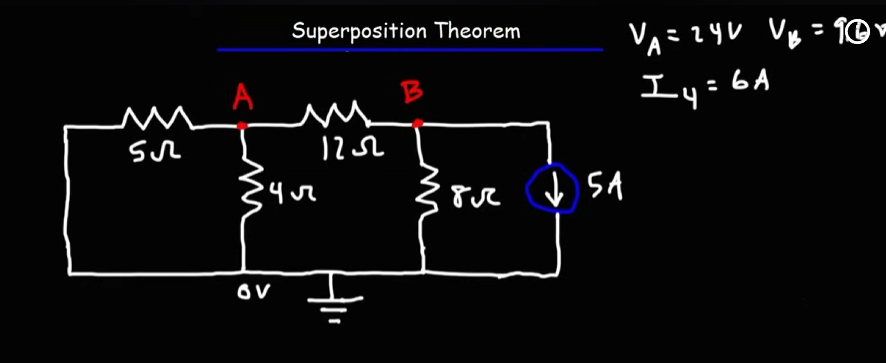
Time to solve for the $5A$ source now. Notice that the other side of the circuit, the $60V$ source has been replaced with a short circuit.

This time, we will perform nodal analysis that uses KCL, instead of mesh analysis, that uses KVL.

Before we proceed:

What exactly are the rules for nodal analysis?

When we do nodal analysis, we:

• forget about “which way” the wire bends,
• forget the shape of the circuit,
• and focus purely on connections between nodes and voltage differences.

This means that from the circuit diagram, for a node, even if you see that a resistor precedes a node, the current from the resistor to that node is not considered as "entering", but as leaving the node.

Why? Since from the node's perspective, that's...what the current does practically. It leaves the node.

Unless you explicitly see a current source deliberately entering a source, with a given arrow as well, which will be considered as entering the node, in all other cases, from a nodal analysis point of view, it's just the current leaving the node.

And of-course, the sign convention (default):

• Currents leaving the node = positive.
• Currents entering the node = negative.

Starting off with the first node branch off:

For the $5\mathrm{\Omega }$ resistor, if the current $I_1$ was flowing through the resistor, it would branch off at node A into the currents $I_2$ going to the $4\mathrm{\Omega }$ resistor and current $I_3$ going to the $12\mathrm{\Omega }$ resistor.

Same logic: $I_1=I_2+I_3$, or $I_3=I_1-I_2$.

The equation would be:

or:

That would be valid mathematically if we were still thinking from a KVL perspective.

However from Why is the sum zero? we know that:

So,

Now, you might be wondering? Why do the $5\mathrm{\Omega }$ and $4\mathrm{\Omega }$ resistors share the same voltage despite being connected in series? And what's up with the voltage difference of nodes A and B for the $12\mathrm{\Omega }$ resistor?

Well, I'd say you got got, since you fell for a very neat optical illusion, that even I did too at first, compounded with a missing definition.

First off,

• The voltage for an electrical component is determined by the electric potential difference between it's two terminals.

If you notice the ends of the $5\mathrm{\Omega }$, $4\mathrm{\Omega }$ and the $12\mathrm{\Omega }$ resistors.

They actually are like this:

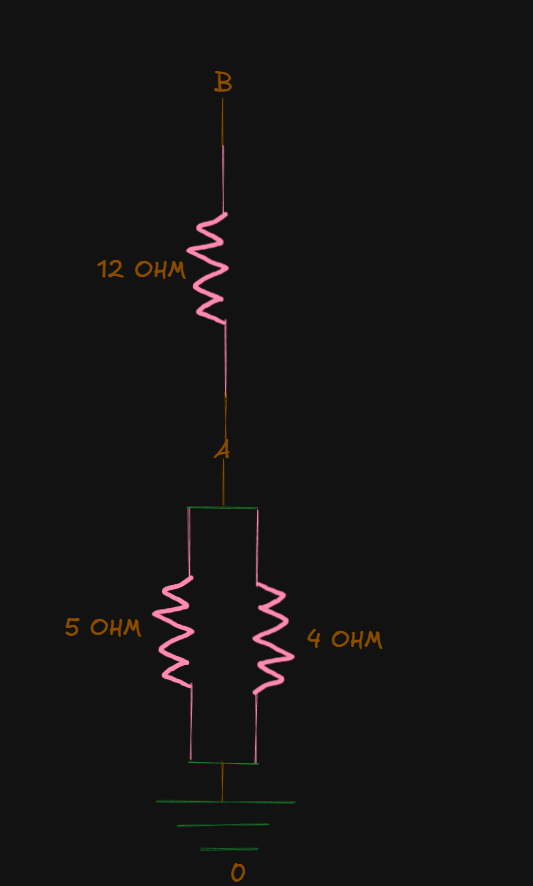
So, the $5\mathrm{\Omega }$ and $4\mathrm{\Omega }$ resistors are in a parallel connection to each other, not series, so they share the same voltage.

Now, for the $5\mathrm{\Omega }$ and $4\mathrm{\Omega }$ resistors the voltage would be: $V_A-0=V_A$.

And for the $12\mathrm{\Omega }$ resistor it would be: $V_A-V_B$.

Now that all confusions are cleared up, let's proceed to the second node.

For node B:

You might be wondering: Why $V_B-V_A$ instead of $V_A-V_B$ ?

To answer that:

If you used the same sign form $V_A-V_B$ in both node equations, you’d be implying the current leaves both nodes simultaneously in the same direction — which violates KCL (current can’t flow out of both ends of a resistor at once).

You can think of it like two people describing the same tug-of-war rope:

• Person A says, “I’m pulling on the rope to the right with 10 N.”

• Person B says, “I’m pulling on the rope to the left with 10 N.”

They’re describing the same force, just in opposite reference directions — exactly like:

$V_A-V_B$ vs $V_B-V_A$.

The extra 5 amps comes from the current of $5A$ where the current leaving the upper branch of node B, goes through the $5A$ source then goes to the ground.

So, we have the two equations:

and:

From the first equation:

From the second equation:

Applying the value of $V_B$:

Now:

Thus,

Total currents and voltages

Now, it's time to add up the current and voltage values obtained from both sources:

From first half (60 V source), we had:

$V_A=24V$
$V_B=9.6V$
$I_5=7.2A$
$I_4=6A$
$I_{12}=1.2A$
$I_8=1.2A$

From the second half (5A source), we have:

$V_A=-4V$
$V_B=-25.6V$
$I_5=-0.8A$
$I_4=-1A$
$I_{12}=1.8A$
$I_8=-3.2A$

Notice a discrepancy?

You might be thinking,

For the 60V source the current values for $I_{12}$ and $I_8$ were same, since they are connected in series, $I_{12}$ has ends from nodes A to B, $I_8$ has ends from node B to ground. Why are the current values different this time for these two?

That's because of how the circuit structure(topology) changed when we added and removed the sources in each half of the calculation.

The resistors were in series in both cases, but the circuit topology changed during the 5A source, node B became a junction instead since the current from node A arrived at node B, and further branched off, one part to the $8\mathrm{\Omega }$ resistor the other to the 5A source, which fixes that part of the current to 5A only. The split caused the resistors to now have different current values. In case of the 60 V source the path from node B was a dead end due to the circuit being open, so the only path was to the $8\mathrm{\Omega }$ resistor, thus allowing both resistors to have the same current value.

So, finally

(using Ohm's law here.) (same as $7.2+0.8=8.0A$) (the minus sign is ignored since that just denotes direction of current and the magnitude of current cannot be positive)

same as $6-1=5A$ (why the minus is here? Since opposing currents resulted in the 5A current and the resulting magnitude is positive and the direction is the same as the dominating magnitude, which is downwards).

Can also be obtained by: $\frac{12}{20-16}=\frac{12}{4}=3A$

Also obtainable by: $1.2-3.2=2A$ (the dominating current direction is upwards).

And that's exactly as the values in the video:

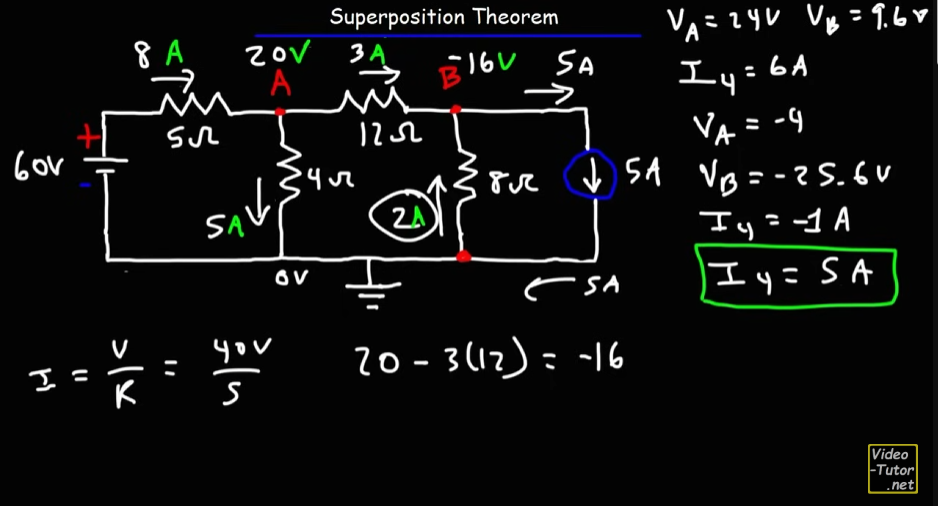
And that's it for the superposition theorem! This numerical hopefully cleared up a lot of concepts and potential confusions underlying the analysis of DC circuits using KCL and KVL too.

https://www.youtube.com/watch?v=EX52BuZxpQM (same video)

There's another example in the video, which you can follow up with for even more practice!

Advantages and Limitations of Superposition Theorem

Advantages

• Simplifies analysis of complex multi-source circuits​

• Each single-source circuit is easier to solve​

• Useful for understanding individual source contributions​

Limitations

• Can be time-consuming if many sources exist​

• Not applicable to nonlinear circuits (with diodes, transistors, etc.)​

• Cannot directly calculate power (must find voltage/current first, then calculate power)​

Thevenin's Theorem

Thevenin's Theorem states that any linear two-terminal network containing voltage sources, current sources, and resistors can be replaced by an equivalent circuitconsisting of a single voltage source $(V_{Th})$ in series with a single resistor ($R_{Th}$).

The Thevenin equivalent circuit

Original complex circuit $\to$ Simplified to: $V_{Th}$ in series with $R_{Th}$.

where:

• $V_{Th}$ is the Thevenin voltage, Open-circuit voltage across the terminals.

• $R_{Th}$ is the Thevenin resistance, equivalent resistance seen from the terminals with all sources deactivated.

How to find the Thevenin Equivalent Circuit?

Step 1: Identify the two terminals (a-b) across which you want the equivalent circuit​.

Step 2: Remove the load (usually a load resistor) (if any) connected between terminals a-b​.

Step 3: Find $V_{Th}$ (Thevenin voltage):​

• This is the open-circuit voltage ($V_{oc}$) across terminals a-b​

• First use superposition theorem to find out the voltages and currents from individual sources (in most cases that will be the case), then add them up, focus specifically on the voltages of the two terminals. Use any circuit analysis method (KVL, KCL, nodal, mesh)

• Thus, $V_{Th}=V_A-V_B$, the difference of the voltages of the two terminals.

Step 4: Find $R_{Th}$ (Thevenin resistance):​

If only independent sources:

• Deactivate all independent sources:​

  • Replace voltage sources with short circuits.​

  • Replace current sources with open circuits.​

• Calculate the equivalent resistance looking into terminals a-b

If dependent sources are present:

• Find short-circuit current ($I_{sc}$) across terminals a-b

• Then: $R_{Th}=\frac{V_{oc}}{I_{sc}}$

Why Use Thevenin's Theorem?

Advantage: When the load changes frequently, you don't need to re-analyze the entire circuit—just use the Thevenin equivalent with the new load. This is especially useful in power system analysis and electronic circuits.

Norton's Theorem

The Statement

Norton's Theorem states that any linear two-terminal network can be replaced by an equivalent circuit consisting of a single current source $I_N$ in parallel with a single resistor $R_N$.

The Norton Equivalent Circuit

Original complex circuit → Simplified to: $I_N$ in parallel with $R_N$

where:

• $I_N$ is the Norton current - Short-circuit current through the terminals
• $R_N$ is the Norton resistance - Same as Thevenin resistance ($R_{Th}=R_N$).

How to find the Norton Equivalent

The steps are similar to that of finding the Thevenin equivalent

Step 1: Identify the two terminals (a-b) across which you want the equivalent circuit​.

Step 2: Remove the load (usually a load resistor) (if any) connected between terminals a-b​.

Step 3: Find $I_N$ (Norton Current):

• This is the short-circuit current ($I_{sc}$) that flows when terminals a-b are shorted.

Step 4: Find $R_N$ (Norton Resistance):

• Same procedure as finding $R_{Th}$
• $R_N=R_{Th}$

Relationship between Thevenin and Norton

These two theorems are equivalent and interchangeable through source transformation:

• $V_{Th}=I_N\times R_{Th}$
• $I_N=\frac{V_{Th}}{R_{Th}}$
• $R_{Th}=R_N$

Example

https://www.youtube.com/watch?v=-kkvqr1wSwA (This video explains both Thevenin's and Norton's Theorem)

This is the given circuit. Notice that we have two sources, one a 100V battery, a 7A source. And also a load resistor.

We have two terminals A and B of the load resistor.

Step 1: Finding the Thevenin resistance $R_{Th}$

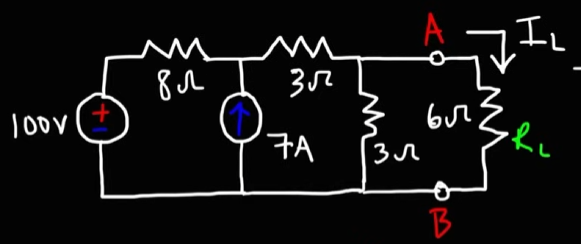
• Remove the load resistor
• Replace voltage source with closed circuit
• Replace current source with open circuit

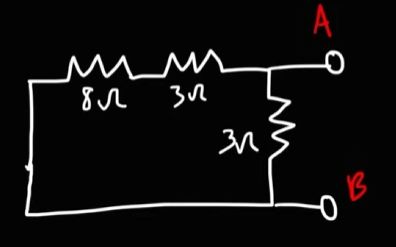
Now we simply analyze the circuit to find the total resistance, which will be our Thevenin Resistance

Now, the $8\mathrm{\Omega }$ resistor is in series with the $3\mathrm{\Omega }$ resistor and their combined resistance is in parallel (due to the 100V battery gone and a single wire connecting both the resistors, they now share the same terminals) with the other $3\mathrm{\Omega }$ resistor.

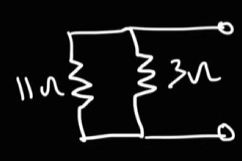
Now, the total resistance or the Thevenin resistance here would be:

Next, use superposition theorem to find the individual voltages and currents from both sources and add them.

For the 100V source:

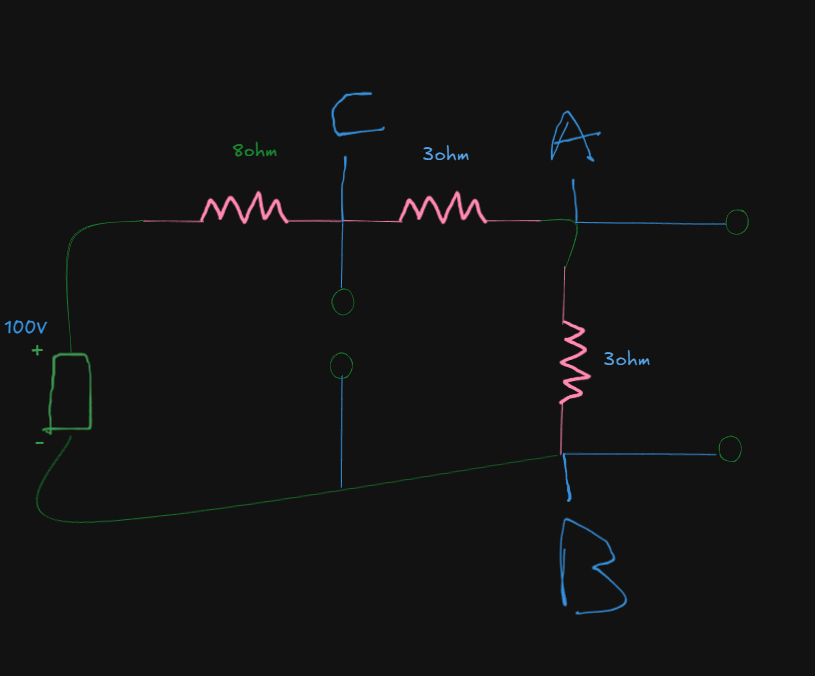
Now, it's not really necessary to go the KVL route here and make things overcomplicated when all we can really do is this:

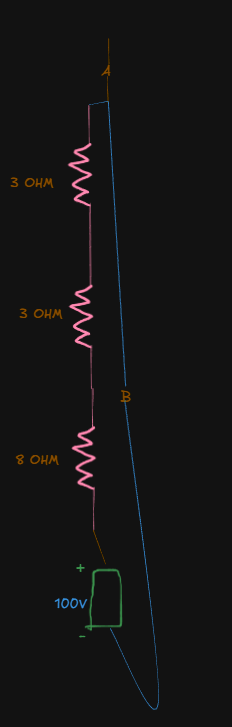
The 3 resistors are in series.

Thus they will share the same current values.

So, we can bundle them into a single resistor of $14\mathrm{\Omega }$.

The current would be: $I=\frac{100}{14}=7.142A$.

For the $8\mathrm{\Omega }$ resistor:

The drop would be: $V_C=100-57.136=42.857V$

For the upper $3\mathrm{\Omega }$ resistor that's:

The voltage drop for node A would be:

Next, for the second $3\mathrm{\Omega }$ resistor, the voltage is the same:

For the voltage drop at node B:

which is basically the negative terminal of the battery, so it's negligible here. This value already confirms our reference point that node B is the ground here.

Now, for the 7A source:

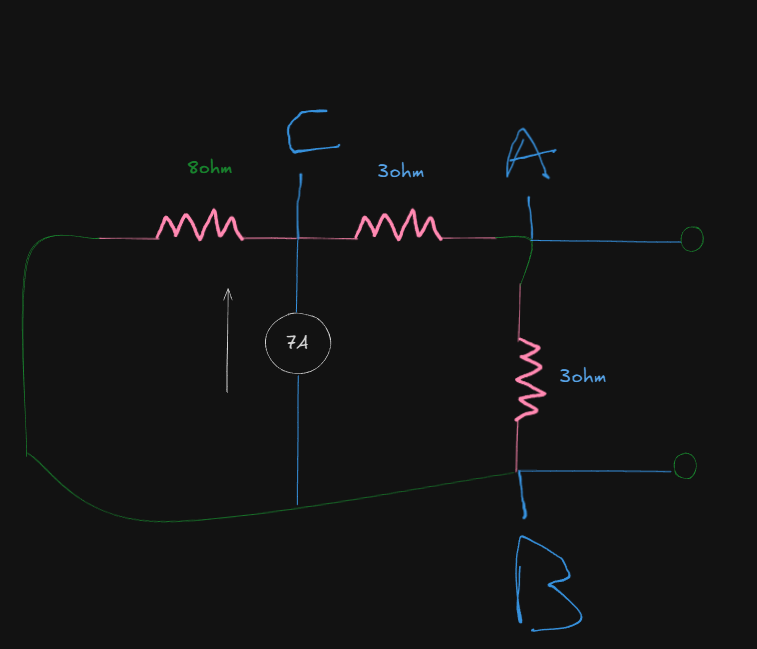
Using nodal analysis here:

If we name the current going into node C from resistor $8\mathrm{\Omega }$ as $I_1$ and the $7A$ resistor is a separate source in itself, the current for the top $3\mathrm{\Omega }$ resistor as $I_2$ and the bottom resistor as $I_3$.

For node C:

Here $V_B$ is our reference point, basically ground so it's just zero.

So, the equation simplifies to:

For node A:

or:

Applying this value in the previous equation:

So:

The current values are:

Just to recap:

From the 100 V source we had:

• $V_C=42.857V$
• $V_A=21.437V$
• The current was $7.124A$ for all 3 resistors.

From the 7A source:

• $V_C=24V$
• $V_A=12V$
• $I_8=3A$
• $I_{3_{top}}=4A$
• $I_{3_{bottom}}=4A$

Superimposing, we get:

So, the Thevenin Voltage $V_{Th}$ is given by:

since ($V_B=0$).

Finally the Norton Current:

The Thevenin Resistance we found out way earlier was:

which is just the same in the video:

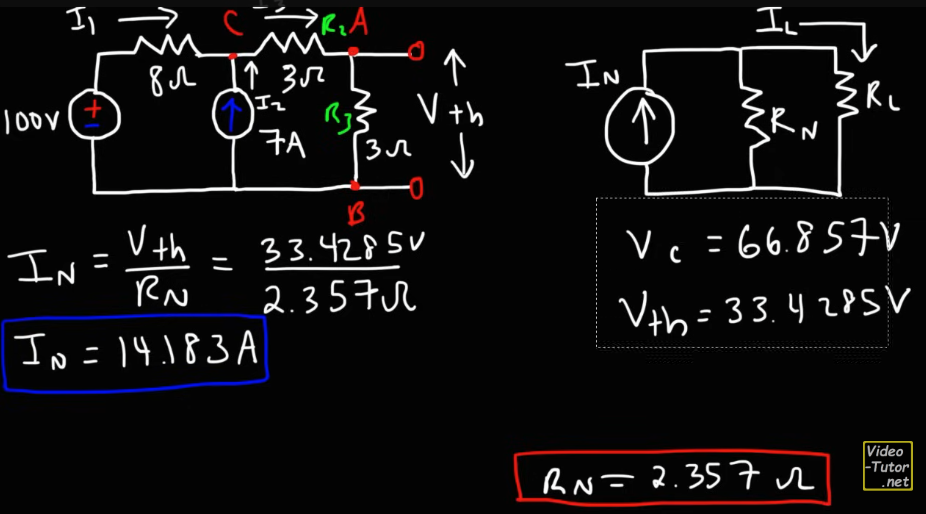
(Ignore minor rounding differences due to different calculators used)

🧭 DC Circuit Analysis — Reasoning Traces & Concept Map

Culmination of all the realizations I made in my own language for all DC circuits.

Core idea: Circuits are networks of nodes and connections, not drawings of wires.
Geometry doesn’t matter — connectivity does.

⚡ 1. Foundational Mindset

• Every resistor is a bridge between two nodes.
• Circuit analysis = applying conservation of charge (KCL) and energy (KVL).
• Pick one reference node (0 V).
  You don’t find ground — you define it.
• Results depend only on voltage differences, never on absolute values.

🔌 2. KCL (Nodal Analysis)

“At every node, the sum of currents leaving = 0.”

1. Assign node voltages: $V_A$, $V_B$, $V_C$, etc.
2. Choose one node as 0 V (reference).
3. For each node:
   • For every resistor connected, write
     I = (V_node - V_other) / R.
     (Defined as leaving the node.)
   • For current sources:
     • +I if it leaves the node.
     • −I if it enters the node.
4. Sum all currents leaving = 0.
5. Solve the resulting equations.
6. A negative result ⇒ actual direction opposite to assumption.

🧠 Mental model:
Each node is like a bubble. The “pressure” (voltage) in it adjusts until no net flow of charge occurs.

🔁 3. KVL (Mesh Analysis)

“Around any closed loop, total voltage rises and drops = 0.”

1. Identify independent meshes (loops).
2. Assign each a loop current (CW or CCW).
3. For each loop:
   • Write ΣV = 0, summing voltage drops and rises.
   • For resistors: V = I × R.
   • For shared resistors: use the difference (I1 − I2).
4. Solve the system for loop currents.
5. A negative value = actual direction opposite to your guess.

🧠 Mental model:
Each loop is an energy story — sources give, resistors take, and the “budget” balances to zero.

🧮 4. Superposition Theorem

“The total response = sum of each source acting alone.”

1. Identify all independent sources.
2. For each subcase:
   • Keep one source active, turn others off:
     • Voltage source → short circuit.
     • Current source → open circuit.
   • Solve for desired currents/voltages.
3. Add results algebraically (consider signs).
4. Superposition applies to linear circuits only.

🧠 Mental model:
Each source plays its own “melody”; the circuit’s behavior is the harmony of all their songs.

🔋 5. Thevenin & Norton Equivalents

“Simplify any linear network into a single source and a single resistor as seen from two terminals.”

Finding R_Th (or R_N)

1. Deactivate all independent sources:
   • Voltage source → short.
   • Current source → open.
2. Look into the circuit from the terminals (A–B).
3. Combine resistors using series/parallel to find the equivalent resistance.

Finding V_Th

1. Reactivate all sources.
2. Remove the load (open circuit across A–B).
3. Use KCL/KVL or superposition to find the open-circuit voltage:
   V_Th = V_A − V_B.

Finding I_N

$I_N=\frac{V_{Th}}{R_{Th}}$

🧠 Mental model:
From the load’s perspective, the entire circuit behaves like one simple source with internal resistance.

🔄 6. Sign & Direction Logic

• You’re free to assume current directions and voltage polarities.
  The math will correct you if wrong.
• A negative current just means flow is opposite to your assumption.
• Physical intuition (current flows high → low potential) is for checking, not defining.
• Stick to one consistent sign convention per node.

🪄 7. Topology Tips

• Series: Same current through all elements (single path).
• Parallel: Same voltage across all elements (share both endpoints).
• If two resistors of equal value connect a node to two other points,
  that node’s voltage is halfway between them.
• Deactivating sources can change topology — always redraw.
• Symmetry in resistors → look for proportional voltage relations.

🧠 8. Grounding Principle

• “Ground” = the node you define as 0 V.
• Choose the node:
  • with the most connections, or
  • that returns to the main source’s negative terminal.
• Any node can be reference — only voltage differences matter.

🎯 9. Meta Reasoning Checklist

• ✅ Redraw complex circuits to clarify nodes.
• ✅ Label every node and current direction before writing equations.
• ✅ Check if sources change circuit connectivity when deactivated.
• ✅ Always write equations symbolically first — substitute numbers later.
• ✅ When stuck, use energy/charge conservation intuition instead of blindly solving.

🧩 10. Quick Cheat Lines

• KCL: “All roads lead to 0 net current per node.”
• KVL: “Every loop pays its energy bill in full.”
• Superposition: “Each source plays its solo; the total is the symphony.”
• Thevenin/Norton: “Circuit shrink rays for linear worlds.”
• Ground: “You don’t find it — you define it.”
• Signs: “Direction is just language; the math tells the truth.”

✅ 11. Summary of Key Equivalences

Final mindset:
Circuit diagrams show the physical world; nodal equations describe the logical world.
Once you can switch between the two, you’ve mastered DC circuit reasoning.