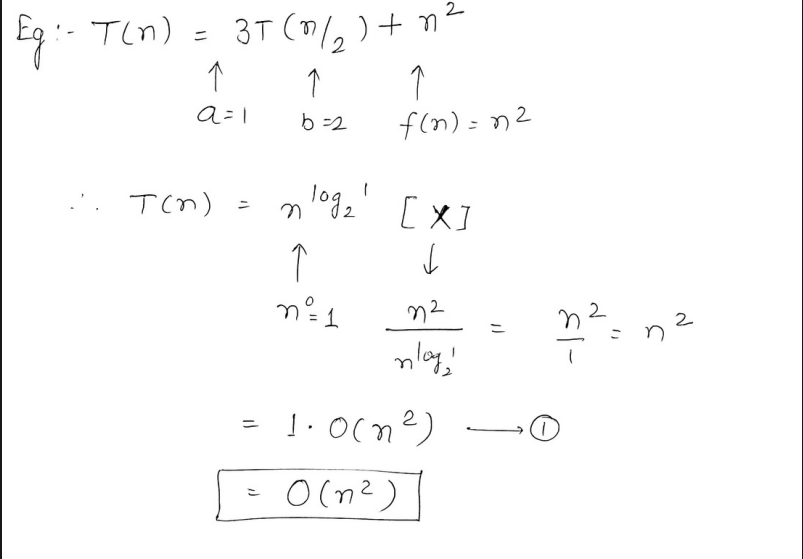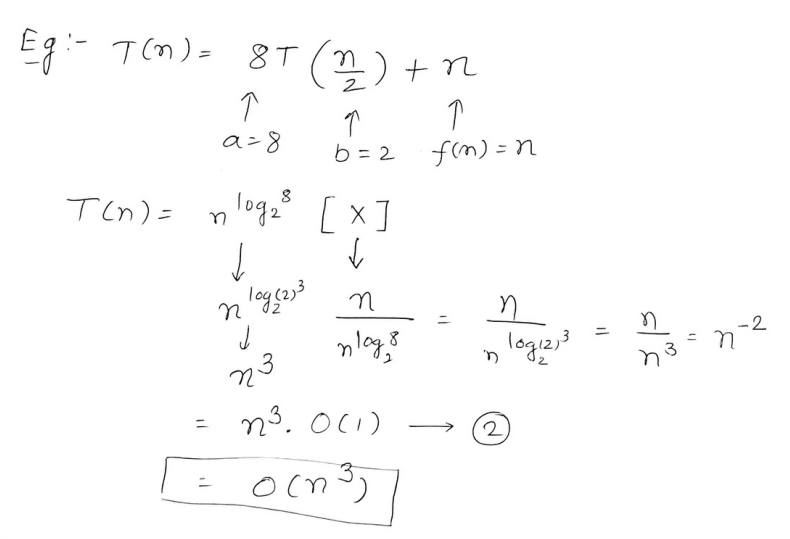What is an algorithm?

Algorithm vs Program

Complexity Bounds and Asymptotic Notations

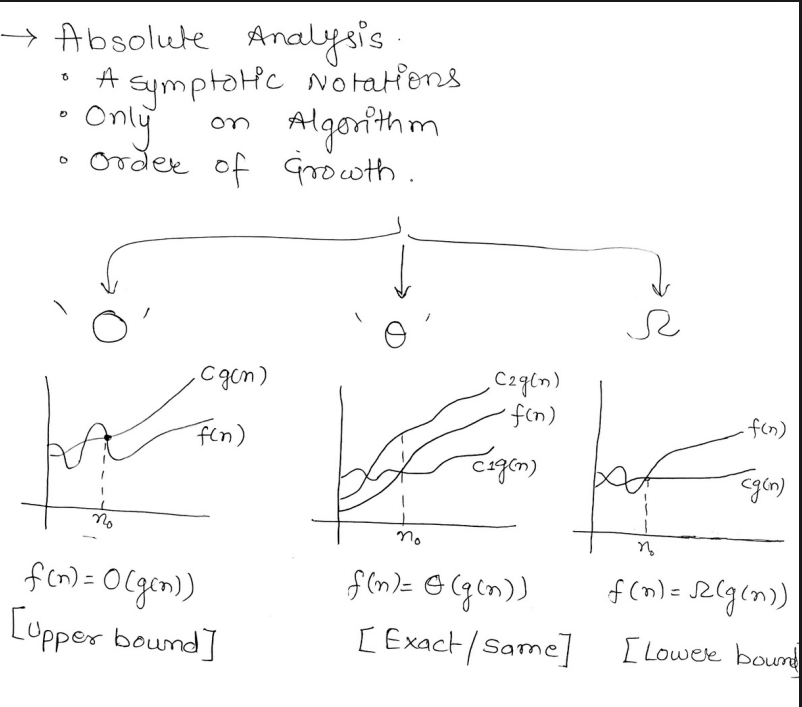
So there are 3 asymptotic notations,

1. Big - O (pronounced as Big oh)
2. Big - $\mathrm{\Theta }$ (pronounced as Big theta)
3. Big - $\mathrm{\Omega }$ (pronounced as Big omega)

These are used in comparison of ranges, which happen to be either have an

1. Upper bound
2. Exact/same bound
3. Lower bound

For example in the first graph we have the function $g(n)$ is the upper bound for $f(n)$ which means when values of n>$n_0$ , $f(n)$ will never be greater than $g(n)$ , denoted by O.

Therefore $f(n)$ = O($g(n)$)

In the second graph, for values of n>$n_0$ , $f(n)=g(n)$ , which is denoted by $\mathrm{\Theta }$ .

Thus, $f(n)$ = $\mathrm{\Theta }(g(n))$

In the third graph, for values of n>$n_0$ , $g(n)$ will always be lesser than $f(n)$, which is denoted by $\mathrm{\Omega }$.

Thus $f(n)=\mathrm{\Omega }(g(n))$.

These were the Big Notations.

There also exist small notations.

Here only small-o (small oh) and small omega exist, since only lower or greater bounds are defined by small notations, exact notations cannot be defined using small notations.

$\omega$ is small omega, $\mathrm{\Omega }$ .

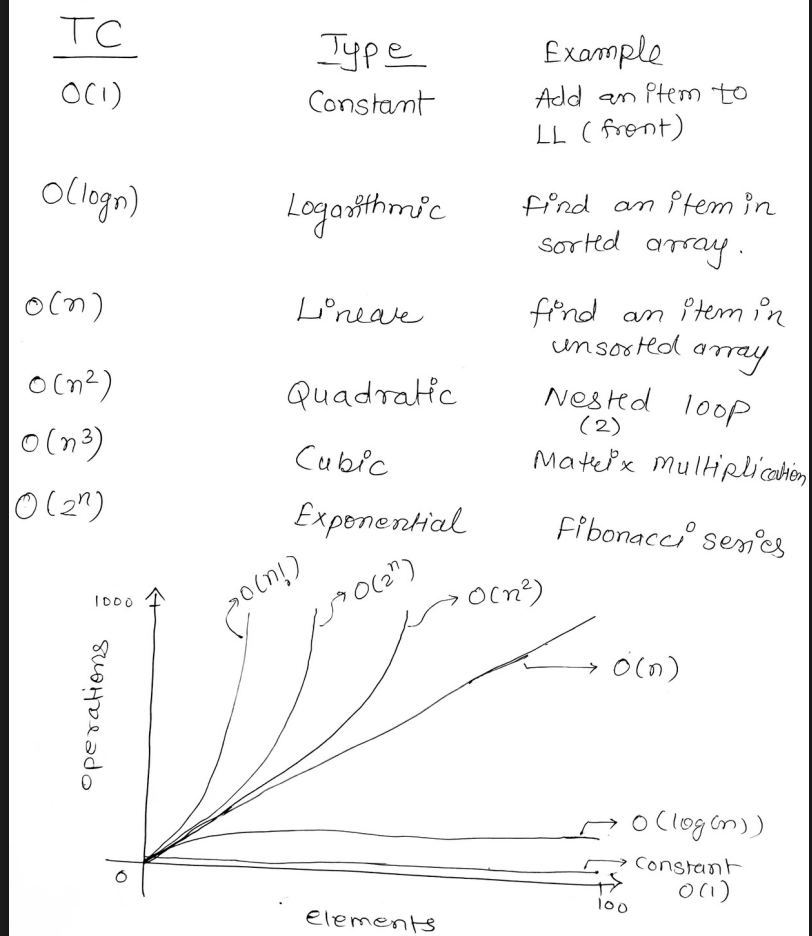
Types of Time Complexity.

Recurrence Relations

For example : The time complexity of the binary search algorithm.

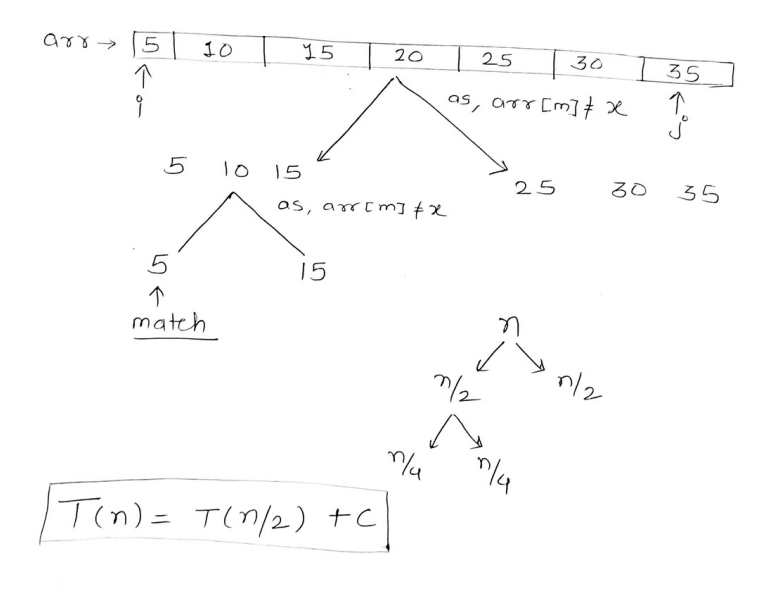
The expression $T(n)=T(n/2)+C$ is a recurrence relation and it is the recurrence relation of the binary search algorithm.

There are two major methods to solve a recurrence relation.

1. Substitution Method
2. Master Theorem

1. The Substitution Method

So we have the recurrence relation

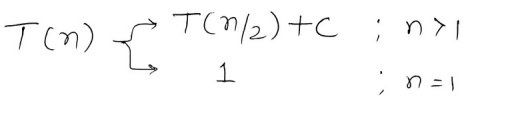
So we start by substituting $n=n/2$

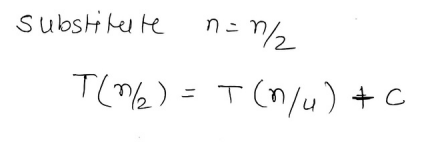
Thus $T[(n/2)/2]=T(n/4)+C$ ....... (i)

And then we repeat the process again for $T(n/4)$ .

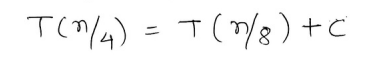
....... (ii)

Then we substitute the value of equation (i) in the original recurrence relation $T(n)=T(n/2)+C$ :

And we do the same for equation (ii) as well.

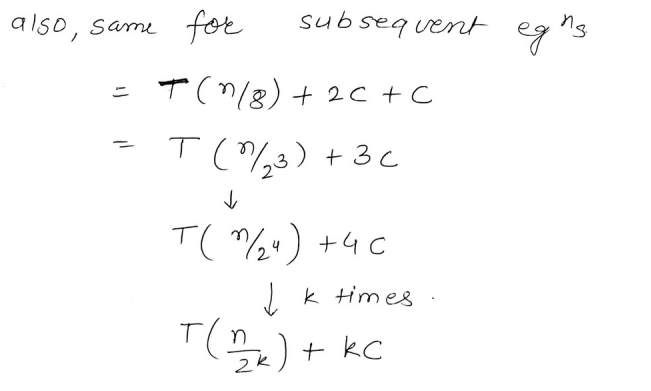
And thus we see that a pattern approaches with this equation :

$T(n/2^k)+kC$ .....(iii)

Let's set equation $n/2^k$ equal to 1.

Therefore, $n/2^k$ = 1

or $2^k$ = n.

Therefore we get : $T(n/n)+kC$

or $T(1)+kC$

This gets reduced to

$1+logn.C$

which is further reduced to

O($log(n)$)

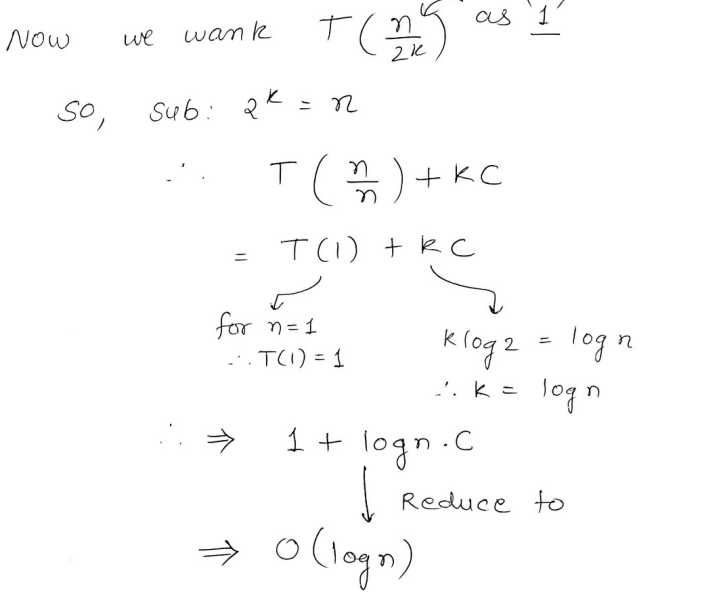
2. Master Theorem.

This theorem is faster to use than the substitution method however it cannot be applied to all recurrence relations .

There are certain conditions which need to be fulfilled for the Master Theorem to be fulfilled.

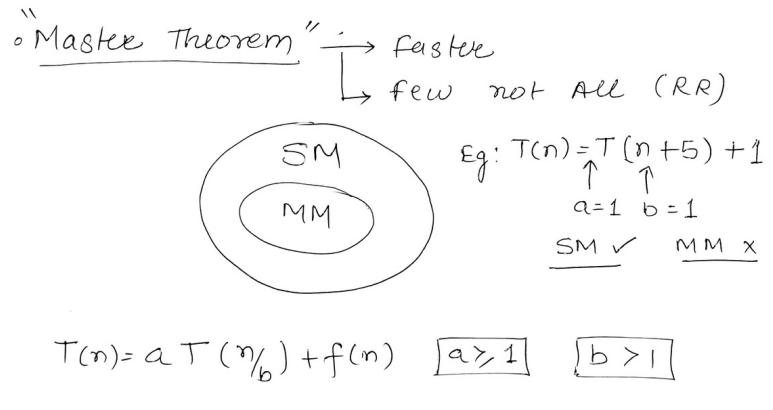
So if the recurrence relation is of the type :

$T(n)=aT(n/b)+f(n)$

where $a\ge 1$ and b > 1

Therefore, Master theorem can be applied to this recurrence relation.

In the problems/limitations section those are the factors which prevent Master theorem from working on a recurrence relation.

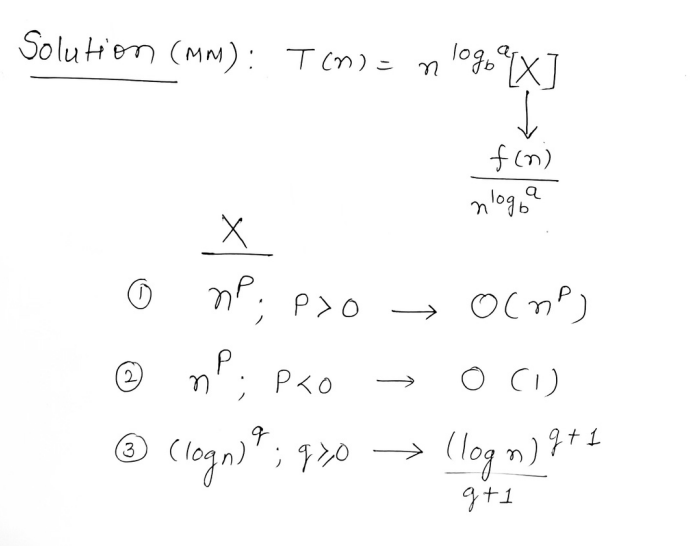
Now, we need to convert that recurrence relation to the form of

or $f(n)/n^{log{b}^a}$

where if X = $n^P,P>0$ then it is the upper bound O($n^P$)
if X = $n^P,P<0$, then it is linear time, O(1)
if X = $(logn{)}^q,q\ge 0$ then it becomes $(logn{)}^{q+1}/(q+1)$