Web Mining -- Data Mining -- Module 5

#Semester-6 #Data-Mining #Web-Mining

Index

  1. Mining the Web Page Layout Structure
  2. Web Link Mining
  3. 📊 1. PageRank Algorithm (Used by Google)
  4. 2. HITS Algorithm (Hyperlink Induced Topic Search)
  5. Mining Multimedia Content on the web (brief overview)
  6. Automatic classification of documents on the web
  7. 1. Support Vector Machines (SVM)
  8. 2. K-NN algorithm (K-Nearest Neighbours)

🌐 What is Web Mining?

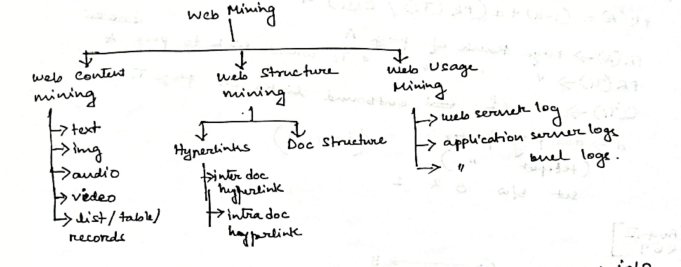
Pasted image 20250503141751.png

Web Mining is the process of using data mining techniques to extract knowledge from web data, which includes:

🔍 Three Main Types of Web Mining

  1. Web Content Mining

    • Extracting useful information from the content of web pages.
    • Example: Identifying topics in blog posts, product descriptions, etc.
    • Techniques: Natural Language Processing (NLP), Information Retrieval.

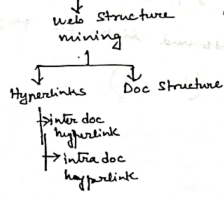
  2. Web Structure Mining

    • Discovering structure and relationship between web pages (like hyperlink patterns).
    • Example: Google’s PageRank uses this to rank pages.
    • Techniques: Graph theory, Link analysis.

  3. Web Usage Mining

    • Understanding user behavior by analyzing web logs, clickstreams, or sessions.
    • Example: Recommender systems, heatmaps.
    • Techniques: Clustering, Association Rules, Sequential Pattern Mining.

Mining the Web Page Layout Structure

Pasted image 20250503141856.png

🧱 What is "Web Page Layout Structure Mining"?

This refers to analyzing the structural organization of a webpage — not the content or links, but how it's visually and semantically arranged using HTML tags and styling (e.g., <div>, <header>, <section>, <nav>, <footer>, etc.).

🎯 Why Do We Mine Layout Structure?

🔍 Key Techniques:

  1. DOM Tree Analysis

    • The Document Object Model (DOM) represents the HTML layout as a tree.
    • Each tag is a node.
    • Layout structure mining inspects this tree to:
      • Find the main content block
      • Remove boilerplate code (ads, navbars, etc.)

  2. Tag Path Patterns

    • Repeated tag patterns (like repeated <div class="item">) often indicate structured data, such as product listings or blog entries.

  3. Visual Segmentation (e.g., VIPS Algorithm)

    • Uses visual layout (CSS, screen position) to divide the page into logical segments.
    • Helps identify what's central or peripheral.

  4. Tree-based Similarity

    • Comparing trees across multiple pages on a website to identify template structure.

🛠️ Real-world Use Cases

Example -- DOM Tree Analysis

Let's say we have a sample HTML webpage:

<html>
  <body>
    <header>
      <h1>My Blog</h1>
    </header>
    
    <nav>
      <ul>
        <li>Home</li>
        <li>About</li>
      </ul>
    </nav>
    
    <div class="content">
      <div class="post">
        <h2>Post 1</h2>
        <p>This is the first blog post.</p>
      </div>
      <div class="post">
        <h2>Post 2</h2>
        <p>This is the second blog post.</p>
      </div>
    </div>
    
    <footer>
      <p>Contact us</p>
    </footer>
  </body>
</html>

The DOM Tree for this would be:

html
└── body
    ├── header
    │   └── h1
    ├── nav
    │   └── ul
    │       ├── li
    │       └── li
    ├── div (class="content")
    │   ├── div (class="post")
    │   │   ├── h2
    │   │   └── p
    │   └── div (class="post")
    │       ├── h2
    │       └── p
    └── footer
        └── p

Mining this tree would tell us this information:

Region Detected as Reason
<header> Boilerplate (title/banner) Appears on all pages, not content-specific
<nav> Boilerplate (navigation) Contains menu links
.post blocks Main Content Repeating tag path → dynamic data
<footer> Boilerplate (footer info) Same across pages

We would get a more professional output as:

{
  "main_content": [
    {
      "title": "Post 1",
      "text": "This is the first blog post."
    },
    {
      "title": "Post 2",
      "text": "This is the second blog post."
    }
  ],
  "boilerplate": {
    "header": "My Blog",
    "footer": "Contact us",
    "nav": ["Home", "About"]
  }
}

This separation helps when you want to:

Web Link Mining

Web Link Mining focuses on discovering patterns and structures in the hyperlinks between web pages. The idea is that links carry implicit human judgment — people link to what they find relevant or authoritative.

There are two primary tasks:

  1. Identifying authoritative sources (important pages)
  2. Discovering good hubs (pages that link to many good sources)
Link Type Description
In-links (Backlinks) Links pointing to a page
Out-links Links from a page to others
Reciprocal Links Mutual linking between pages

We only got two, don't worry.

📊 1. PageRank Algorithm (Used by Google)

🧠 Core Idea:

A page is important if important pages link to it. This is a recursive definition of importance.

📌 Formula:

PR(A) = 1 − dN + d ∑i∈ In(A) PR(i)L(i)

where:

🔄 How It Works:

  1. Initialize each page's PR to 1N
  2. Iterate the formula above multiple times (until values stabilize)
  3. Pages with high PR are considered more authoritative

Example

🌐 Web Graph Setup

Assume we have 4 web pages: A, B, C, D.

Their link structure:

We can visualize it like this:

flowchart TD;
	A<-->C
	A-->B
	B-->C
	D-->C

So total number of pages, N = 4

So initial PageRank PR = 14 = 0.25 for all pages.

And we set the damping factor d = 0.85.

Now it's time to iterate.

Iteration 1

In-links : C (An in-link is the incoming link from a page, to the page whose page rank we are evaluating).

Out-links: C has only 1 out-link, going to A

In this case, for A, the link coming to A is from C.

So since there's only one page that's linking to A, C and C has only 1 out-link

The page rank of A will be:

PR(A) = 1 − 0.854 + 0.85 × 0.251⟹PR(A) = 0.0375 + 0.2125 ≈ 0.25

In links: A
Out links: A has two out-links, one going to B, and another one to C

So, Page Rank of B will be:

PR(B) = 1 − 0.854 + 0.85 × [ 0.252 ]⟹PR(B) = 0.0375 + 0.10625 ≈ 0.14375

In-links: A, B, D.

Out-links: A = 2, B = 1, D = 1

So , PageRank of C will be:

PR(C) = 1 − 0.854 + 0.85 × [ 0.252 +0.143751 + 0.251 ]

Skipping the calculations this time, I'll leave that to you guys,

PR(C) ≈ 0.56875

In-links : None

So,

PR(D) = 0.0375 + 0 = 0.0375

📊 Result After Iteration 1:

Page PageRank
A 0.25
B 0.14375
C 0.56875
D 0.0375

We’d normally repeat for 10–20 iterations or until values stabilize.

In PageRank, "stabilization of values" means that the PageRank scores of all pages stop changing significantly between iterations — they converge.

📉 What Stabilization Looks Like:

Let’s say we have 3 pages A, B, and C. Initial ranks are:

After 1st iteration:
PR(A) = 0.42, PR(B) = 0.29, PR(C) = 0.29

2nd iteration:
PR(A) = 0.40, PR(B) = 0.30, PR(C) = 0.30

3rd iteration:
PR(A) = 0.399, PR(B) = 0.3005, PR(C) = 0.3005

Eventually:

✅ Why is this important?

Because without stabilization:

✅ Interpretation:

Use Case Description
Search Engines Improve ranking of results (PageRank, HITS)
Web Structure Analysis Understand influence and centrality
Spam Detection Detect link farms and manipulation
Community Detection See which sites/pages cluster together

📌 HITS Overview

You can think of it like:

🔁 Basic Working

  1. Start with a base set of pages (could be from a search result).

  2. Initialize all hub and authority scores to 1.

  3. Iterate:

    • Update authority score of each page:
      Sum of hub scores of pages linking to it
    • Update hub score of each page:
      Sum of authority scores of pages it links to

  4. Normalize scores (so they don’t explode).

  5. Repeat until convergence (stabilization).

🧠 Intuition

Example

Let's understand this with the help of an example.

flowchart TD;
	A<-->C
	A-->B
	B-->C
	D-->C

So we have this graph here that represents all our pages and their links.

Step 1: Initialization

Start by setting:

Step 2: Iterate.

Iteration 1

We could continue this for further iterations, but then we will have to normalize the values so that they don't become too big.

📊 Interpretation (after 1 iteration):

Now you might be wondering:

So what happens in further iterations? We use the currently obtained scores, analyze the page again and then keep on adding them up in the same way? If so then in this process only certain pages scores will increase by a higher bound, the rest will be lower, atleast for this graph. You can say that this is the same for the PageRank algorithm as well, the PageRank will just continue to be assigned based on the in-links and out-links and using the obtained values per iteration.

The question is, if we can already see that which pages have the higher and which the lower scores, what is the point of continuing beyond iteration 1?

Well, you are not wrong, but this is why we continue till a certain number of iterations:

🔁 What Happens in Further Iterations?

Yes, in both algorithms:

So for HITS:

And for PageRank:

🤔 Why Not Just Stop at Iteration 1?

You're right — often you can tell who’s "important" early on. But here's why we don’t stop early:

  1. Raw structure can be misleading:

    • Some pages may seem important due to initial connections but fade out as you factor in quality of those connections.
    • Example: A page linked by many unimportant hubs gets a low authority eventually.

  2. Normalization matters:

    • The values may grow (e.g., from 1 → 3 → 5), but we care about relative rankings — we normalize scores to compare fairly.
    • Iteration balances influence and settles values to accurate proportions.

  3. Feedback loop refinement:

    • A good hub points to good authorities → those authorities get reinforced → hubs that point to them get stronger.
    • This feedback loop stabilizes only after a few iterations.

  4. Early patterns aren’t always stable:

    • In larger networks, the node with the highest score after iteration 1 may not stay the highest.
    • Iterations ensure we're not jumping to conclusions based on a single pulse of data.

🧠 Analogy:

Think of it like reputation in a social network:

Mining Multimedia Content on the web (brief overview)

This area focuses on extracting useful information from non-textual content on the web like:

🔍 Key Tasks:

  1. Image Mining

    • Face recognition
    • Object detection (e.g., identifying cars, animals)
    • Feature extraction (edges, colors, patterns)
    • Reverse image search

  2. Video Mining

    • Scene segmentation
    • Action/event detection
    • Emotion recognition from video (e.g., for movies or surveillance)
    • Caption generation (e.g., YouTube auto-captions)

  3. Audio Mining

    • Speech-to-text (transcription)
    • Speaker identification
    • Music genre classification
    • Emotion detection from voice

  4. Metadata Mining

    • Extracting tags, titles, alt-texts
    • Understanding EXIF data in images
    • Using embedded timestamps, geolocation

⚙️ Techniques Used:

💡 Real-World Applications:

🧠 Relevance to Document Classification: Many web documents now contain embedded images, videos, or audio, so understanding and preprocessing these types of content helps improve:

Automatic classification of documents on the web

✳️ What Is It?

Automatic Web Document Classification involves assigning documents (e.g., articles, blogs, reviews) to one or more categories using machine learning or rule-based techniques.

🧰 Techniques Involved:

  1. Preprocessing:

    • Tokenization
    • Stop-word removal
    • Stemming/lemmatization
    • TF-IDF weighting or word embeddings

  2. Feature Representation:

    • Bag of Words
    • N-grams
    • Word2Vec, TF-IDF, BERT (for advanced cases)

  3. Classification Algorithms:

    • Naive Bayes 🟢 (lightweight and common for text) (We already did this)
    • SVM (Support Vector Machine) ⚙️ (effective in high-dimensional spaces)
    • Decision Trees / Random Forests (We did this way back, ID3, CART)
    • Neural Networks (for deeper understanding or longer documents) (Just for context, we will not be covering neural networks, it's way out of depth for us)

🔁 Example Process:

  1. Crawl news articles from the web
  2. Preprocess and vectorize content
  3. Train a Naive Bayes model on labeled categories: Sports, Politics, Tech
  4. Use model to classify new articles automatically

💡 Applications:

Algorithms for classification of web documents

1. Support Vector Machines (SVM)

SVM tries to find the best separating boundary (hyperplane) between two classes in a high-dimensional space (each word = a dimension). It focuses on the "support vectors" — the closest data points to the decision boundary.

⚙️ How It Works:

📋 Example:

Let’s say we’re classifying two categories:

Each document is represented as a vector based on the word frequencies or TF-IDF scores.

🛠️ The SVM finds the boundary such that:

🔍 Why Use It?

Solved example

Let's say we have a classification problem:

Classify whether a document is Tech or Sports based on two word features:

Document "algorithm" freq "goal" freq Class
D1 8 1 Tech
D2 7 0 Tech
D3 6 2 Tech
D4 0 9 Sports
D5 1 8 Sports
D6 2 7 Sports

This is the frequency table of the given words.

We plot these on a 2D graph where:

So:

🔀 SVM Approach:

The goal of SVM is to find the optimal line (in this 2D case) that:

  1. Separates Tech and Sports documents.
  2. Maximizes the margin between the closest points from each class (called support vectors).

Example:

🔍 Classifying a New Document:

Let’s say a new document has:

We plug this into the separating line:

algorithm_freq - goal_freq = 4 - 3 = 1

If the SVM’s learned boundary was:

algorithm_freq - goal_freq = 2.5

Then since 1 < 2.5, it falls on the Sports side → Classified as Sports

2. K-NN algorithm (K-Nearest Neighbours)

🧠 Core Idea:

KNN classifies a document based on the majority label of its K nearest neighbors in the feature space.

⚙️ How It Works:

📋 Example:

Suppose you're classifying a new document that talks about "World Cup, team, final, match".

🔍 Why Use It?

📉 Downside: Computationally expensive for large datasets (must calculate distance to all documents at runtime)

That's it for this module very low effort, only focus on the PageRank and HITS algorithms, rest is just theory.