What is Propositional Logic?

Area of logic that studies ways of joining and/or modifying propositions to form complicated propositions.

Example: "Adam is good at playing football and is representing his college at national level."

This statement could be broken into two propositions P1 and P2:

P1: Adam is good at playing football
P2: is representing his college at national level

Here P1 and P2 are propositional variables

Here the "logical connective" (logical operator) used to form a complicated and meaningful proposition is the AND operator.

Logical Operators

Types of Logical Operators :

Some of these are from ADE.

1. Negation (NOT)
2. Conjunction (AND)
3. Disjunction (OR)
4. Exclusive OR (EX-OR / XOR)
5. Implication ( p --> q )
6. Biconditional ( p <---> q )

For the first 4 logical operators: Quick rundown of basics:

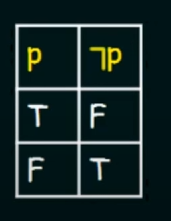
1. Negation :

   Let there be a propositional variable p.

   Denoted by :

   Truth Table :

   

2. Conjunction :

Let there be two propositional variables p and q

Conjunction of p and q will be denoted by:

(p^q)

Truth Table :

3. Disjunction :

   Disjunction of p and q will be denoted by:

   

   Truth table:

   

4. Exclusive-OR:

Denoted by:

Truth Table:

Implication.

"if p then q"

Denoted by : p --> q

Truth table :

+---------------------+
| p | q | p --> q |
+---------------------+
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |

Note:

if the value of first variable (p) is F (false) then no matter what the value of q is, p --> q will always be T (True).

"Easy understandable pseudocode explanation from my end":

if p and q == True then:
p --> q == True

else if p == True and q == False:
p --> q == False

else if p == False:
ignore q.
p --> q == True.

Some examples for implication:

Different ways to represent Implication:

For further clarification : https://www.youtube.com/watch?v=ccz-w2JMsTM&list=PLBlnK6fEyqRhqJPDXcvYlLfXPh37L89g3&index=7

Some more relations of Implications :

Converse, Contrapositive and Inverse

Basically :

Need to remember that :

Implication is p --> q.

Converse is q --> p (mirrored of Implication.)

Contrapositive is: NOT(Converse) (apply negation operator in front of the variables of Converse.)

Inverse is : NOT(Implication) (apply negation operator in front of the variables of Implication.)

Truth Table:

Biconditional Operator.

Let p and q be two propositional variables.
The biconditional statement of the form : p <--> q is the proposition p "if and only if" q

p <--> q is true whenever the truth values of p and q are the same.

Representations of Biconditional Operator.

Precedence of Logical Operators.

The precedence helps us to decide which operator will get evaluated first in a complicated looking compound proposition.

Highest precedence starts from 1 to the lowest being 5.

Translating English sentences into Logical Expressions

Reasons to do this:

1. Removes Ambiguity.
2. Easy manipulation (of logic, not emotions.)
3. Ability to solve puzzles.

How to do this :

Step 1: Find the connectives which are connecting the two propositions together.
Step 2: Rename each part of the sentences on either side of the connectives to a propositional variable.

This should translate to : "If your age is less than 18 years (T) or if you don't have age proof (F), then You are not allowed to watch adult movies".

Answer: ( r s) --> q

Tautology, Contradiction, Contingency & Satisfiability.

1. Tautology: is a compound proposition which is always TRUE.

2. Contradiction : is a compound proposition which is always FALSE.

3. Contingency : is a compound proposition which is sometimes TRUE and sometimes FALSE.

4. Satisfiability: is a compound proposition with at least one TRUE result.

5. Unsatisfiability: is a compound proposition with not even a single TRUE result.

Valid: A compound proposition is valid when it is a tautology.

Invalid : A compound proposition is invalid when it is not a tautology.

Logical Inference : Basic Terminology.

Inference involves two parts :

1. Premise
2. Conclusion

Premise is a proposition on which one would be able to draw a conclusion.

Therefore initially we assume something is true and on the basis of that we draw some conclusions.

Conclusion is a proposition that is reached from the given set of premises.

Basically :

if premise then conclusion

let p = premise, c = conclusion

Then $p\to c$.

Argument

Argument is a sequence of statements that ends with a conclusion (not necessarily true.)

Valid Argument: An argument is valid if and only if it is not possible to make all premises true and one conclusion false.

Rules of inference.

Rules of inference are the templates for constructing valid arguments.

Types of inference rules :

1. Modus Ponens.

   

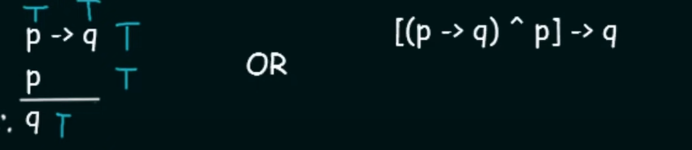
   Here it says that for two propositional variables p and q :

   if p --> q is True AND p is True then the Conclusion will be q (True)

2. Modus Tollens.

   

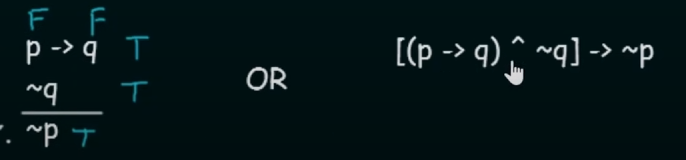
   Here ~ (squiggly symbol) is the same as the negation operator.

   It states that for two propositional variables p and q :

   if p --> q is True AND NOT(q) is True then the Conclusion will be NOT(p) (True).

3. Hypothetical Syllogism

   

   This states that, for three propositional variables p , q and r :

   if p --> q and q --> r then the Conclusion will be p --> r (Transitive property)

4. Disjunctive Syllogism
   

It states that for two propositional variables p and q :

if p or q is True AND NOT(p) is True then the Conclusion will be q

5. Addition

It states that for two propositional variables p and q :
if p is True then the Conclusion will be p or q.

6. Simplification
   

It states that for two propositional variables p and q :

If p AND q is True then the conclusion will be p.

7. Conjunction

   

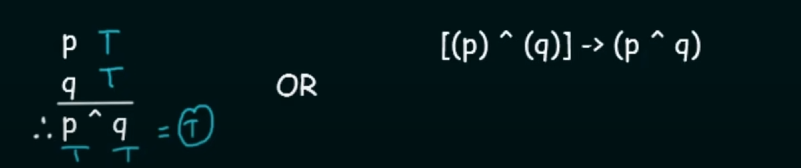
Simply p AND q.

8. Resolution

   

This states that, for three propositional variables p , q and r :

if p OR q is True AND NOT(q) OR r is True then the Conclusion will be q or r.

First Order Logic/ Predicate Calculus.

Used to verify whether an argument is correct or incorrect.

To understand Predicate Logic, we need to understand :

1. Predicates
2. Quantifiers

Predicates

Predicates are statements involving variables which are neither True nor False, until or unless the values of the variables are specified.

They are NOT propositions. (Propositions have a fixed value, either True or False.)

Quantifiers.

Quantifiers are words that refer to quantities such as "some" or "all". It tells for how many elements a given predicate is True.

In English, Quantifiers are used to express the quantities without giving an exact number.

E.g: all, same, many, move, few, etc.

Sentences like: "Can I have some water?" or "Jack has many friends."

Types of Quantifiers:

1. Universal Quantifiers.
2. Existential Quantifiers.

Here "domain" is merely the input of the function Q.

Universal Quantifiers

Definition : The Universal Quantification of some function P(x) is the statement
"P(x)" for all values of x in the domain

Domain or Domain of Discourse

A domain specifies the possible set of values of the variable under consideration.

For example : Let P(x) is the the statement " x+1 > x"

Let us assume that the domain is the set of all positive integers.

Therefore,

P(1): 1+1 > 1 (True)
P(2): 2+2 > 2 (True).

Thus,

Existential Quantifiers

Definition : The existential quantification of a function P(x) is the proposition "There exists an element in the domain such that P(x)........"

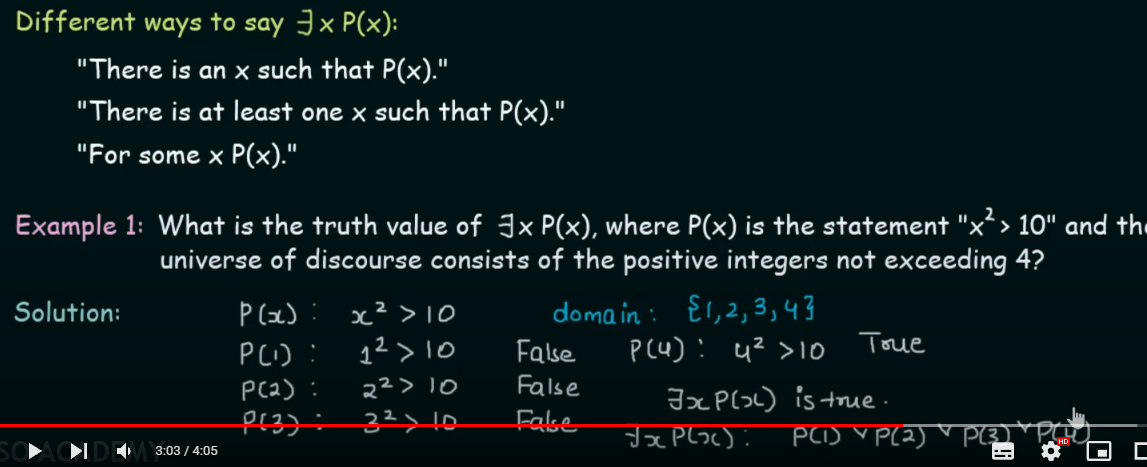
Practice Problems videos :

Propositional Logic Basics

1. https://www.youtube.com/watch?v=scsLVM9i8fg&list=PLBlnK6fEyqRhqJPDXcvYlLfXPh37L89g3&index=13&pp=iAQB
2. https://www.youtube.com/watch?v=otkCaqUhofc&list=PLBlnK6fEyqRhqJPDXcvYlLfXPh37L89g3&index=14&pp=iAQB
3. https://www.youtube.com/watch?v=SBBq-PUvh2c&list=PLBlnK6fEyqRhqJPDXcvYlLfXPh37L89g3&index=15&pp=iAQB

Argument Building using rules of inference [ Important ]

1. https://www.youtube.com/watch?v=28lebQ60TCc&list=PLBlnK6fEyqRhqJPDXcvYlLfXPh37L89g3&index=26&pp=iAQB
2. https://www.youtube.com/watch?v=CqOn_n1PoQ4&list=PLBlnK6fEyqRhqJPDXcvYlLfXPh37L89g3&index=27&pp=iAQB
3. https://www.youtube.com/watch?v=AJe3ATDFIjQ&list=PLBlnK6fEyqRhqJPDXcvYlLfXPh37L89g3&index=28&pp=iAQB

Finding the truth values of predicates

1. https://www.youtube.com/watch?v=Cu9an3Rgd2E&list=PLBlnK6fEyqRhqJPDXcvYlLfXPh37L89g3&index=33&pp=iAQB

Quantifiers

Universal Quantifiers : https://www.youtube.com/watch?v=6Ebxy33e-Wk&list=PLBlnK6fEyqRhqJPDXcvYlLfXPh37L89g3&index=36&pp=iAQB

Existential Quantifiers: https://www.youtube.com/watch?v=YsWn609V6As&list=PLBlnK6fEyqRhqJPDXcvYlLfXPh37L89g3&index=39&pp=iAQB

Expressing Quantifications in English : https://www.youtube.com/watch?v=JY03HH0p14U&list=PLBlnK6fEyqRhqJPDXcvYlLfXPh37L89g3&index=37&pp=iAQB