Context Free Languages and Context-Free Grammar -- Formal Language and Automata Theory
Context Free Language

The main difference between CFL and a Regular language is that of the production rule.
In RL the production rule is not an iteration, that is, it cannot contain an empty symbol.
However in a CFL the production rule is a closure, that is it can contain an empty symbol.
Example





https://www.youtube.com/watch?v=htoFbcwES28&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=72
Derivation Tree
https://www.youtube.com/watch?v=u4-rpIlV9NI&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=73

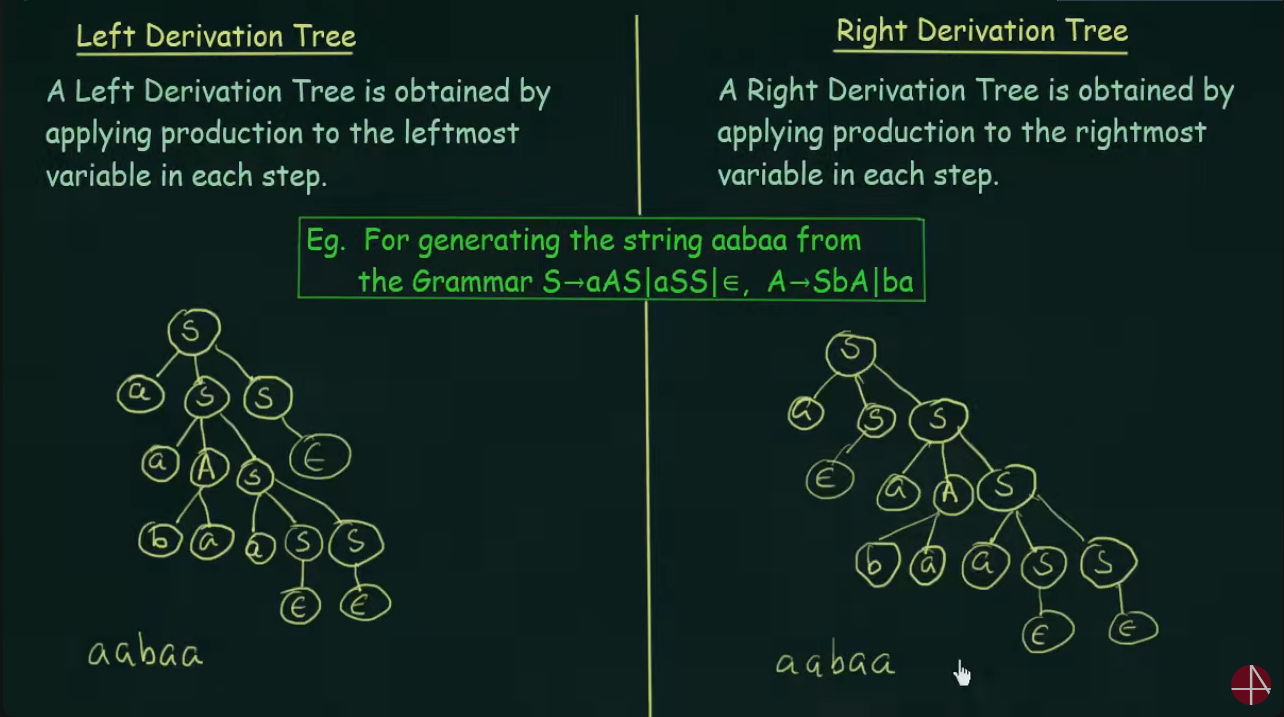
Ambiguous Grammar

Here instead of drawing a tree, the variables were used on the left and right side respectively.
Simplification of CFG : Basics
https://www.youtube.com/watch?v=EF09zxzpVbk&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=75



Example

Phase 1
STEP 1: Make a set of all the terminal symbols (small letters)
And a set of the non-terminal symbols
Now make another set
We add the symbol S in
Therefore,
Continue this if anymore symbols can be added, or else stop.
Phase 2
Make a new Grammar G' which is an equivalent of grammar G, such that :
where V = variables/non-terminal symbols, T = terminal symbols, P = production rules and S = Start symbol
Thus the new production rule P will be : S -> AC, A->a, C->c, E->aA | e .
We ignored B in this rule since B was not included in any of the sets.
Now make a new set
Therefore,
And make another set
Now make another set
Thus,
Notice how E and it's derivations got skipped as well. Since E was redundant.
Thus the new reduced grammar.
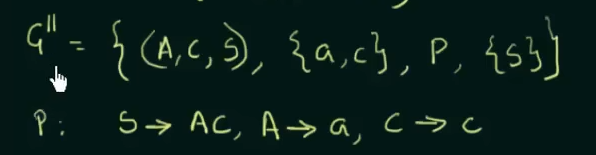
Simplification of CFG : Removal of Unit productions
https://www.youtube.com/watch?v=B2o75KpzfU4&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=76

Example 
Here we need to find the type of productions which are of the type A->B and B->any sort of terminal symbols.
Basically following a whole transitive approach.
So, we can find in the example that :
M -> N and N -> a.
So we can simply substitute M->a instead.
P becomes : S->XY, X->a, Y->Z|b, Z->M, M->a
Again the same applies for Z->M, M->a
We can substitute Z->a instead.
Therefore, P : S->XY, X->a, Y->Z|b, Z->a
Now again the same applies to Y->Z and Z->a.
We can substitute Y->a instead.
Therefore, P : S->XY, X->a, Y->a|b
It may seem that S->X|Y and the same applies here too since X->a, Y->a|b, but we don't modify the start symbol.
Therefore the reduced grammar will be :
P : S->XY, X->a, Y->a|b.
Simplification of CFG (removal of NULL productions)
https://www.youtube.com/watch?v=mlXYQ8ug2v4&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=77

STEP 1: Find all productions in the form of
STEP 2: Replace those productions with just

So basically we will pair the original productions with the non-terminal variables on the left, followed by the | and the replaced variants of the symbol on the right
Therefore in S, we can get the following production:
S -> ABAC
S -> ABC | BAC | BC
For A->aA |
we get : A -> a
similarly for B -> bB |
B -> b
Therefore the new production accordingly will be :
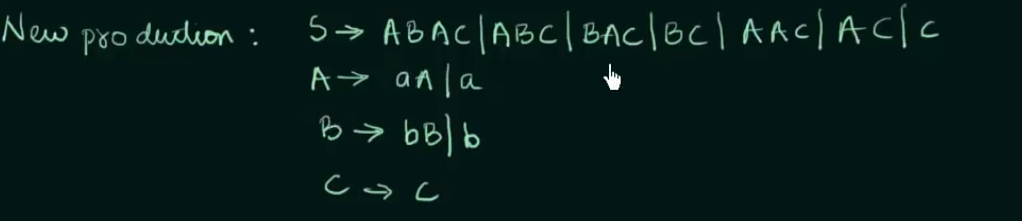
Chomsky Normal Form(CNF) and CFG to GNF conversion
https://www.youtube.com/watch?v=Mh-UQVmAxnw&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=78
In Chomsky Normal Form, we have a restriction on the length of RHS, which is, elements in RHS should either be two variables or a Terminal variable.

where A, B, C are non-terminals and a is a terminal variable.

Conversion of CFG to CNF
https://www.youtube.com/watch?v=FNPSlnj3Vt0&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=79 [Recommended to watch]
Example

Step 1: Check if there is a start symbol on the right hand side of the production
Step 2: If so, then create a production

Step 3: Remove NULL productions

Here we first remove
Step 4: Remove all Unit Productions
 \
\

Here in STEP 4: We found the productions that has more than two variables in RHS.
Thus we have to replace the variables SA with a new one named X.
and in STEP 5: we replaced a with the variable Y.
Both STEP 4 and STEP 5 needed to be enacted since they were violating CNF.
Greibach Normal Form and CFG to GNF conversion



So initially we checked if the given grammar had any unit or null productions [Check Passed]
Next we checked whether the CFG is already in CNF or not. [Check Passed]
So then we simply rename the variables into a form of
Now we need to alter the rules such that there are no non-terminal symbols
Here we find in production 2 that
Thus we need to fix that as follows :
Thus we replace the value of

And we see that the same variable is repeating on the RHS.
This is called left recursion.
Removal of Left recursion

replace the repeating variable with a new variable Z and write with the variable Z once and without it again.
Now write the variable
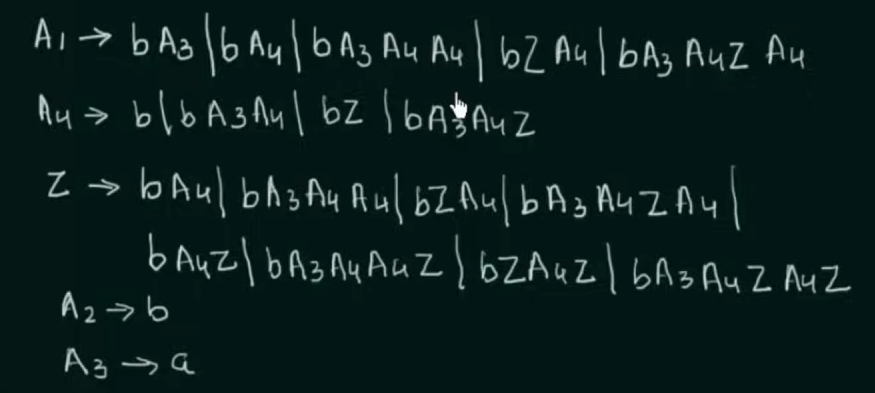
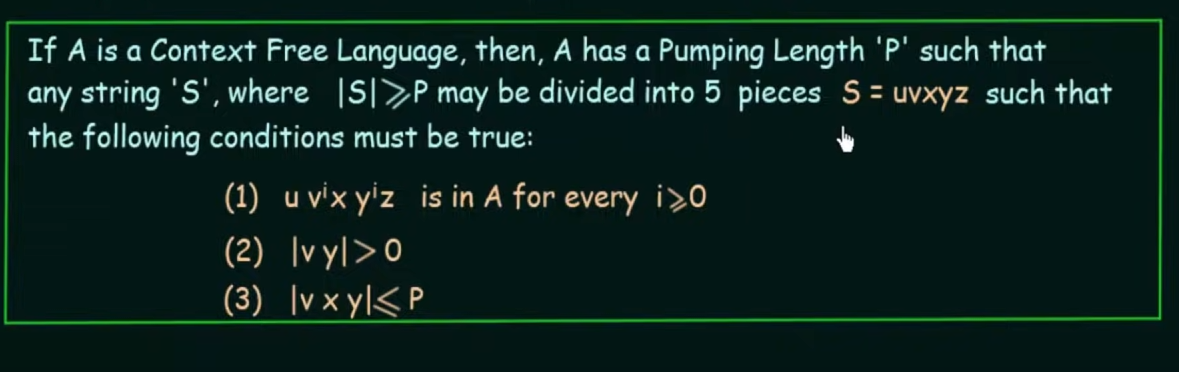
Pumping Lemma for CFL

Same as Pumping lemma for RL, except that the string S needs to be broken down into 5 parts
u, v, x, y, and z .

Example

Let the pumping length P = 4
Therefore we get two cases :


Here we can see that the number of a, b and c are not the same according to the rule of the language.
Thus this language is not context-free
One more example video
https://www.youtube.com/watch?v=DPs8sBcIjs8&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=84
Pushdown Automata



Formal definition
https://www.youtube.com/watch?v=eY7fwj5jvC4&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=87


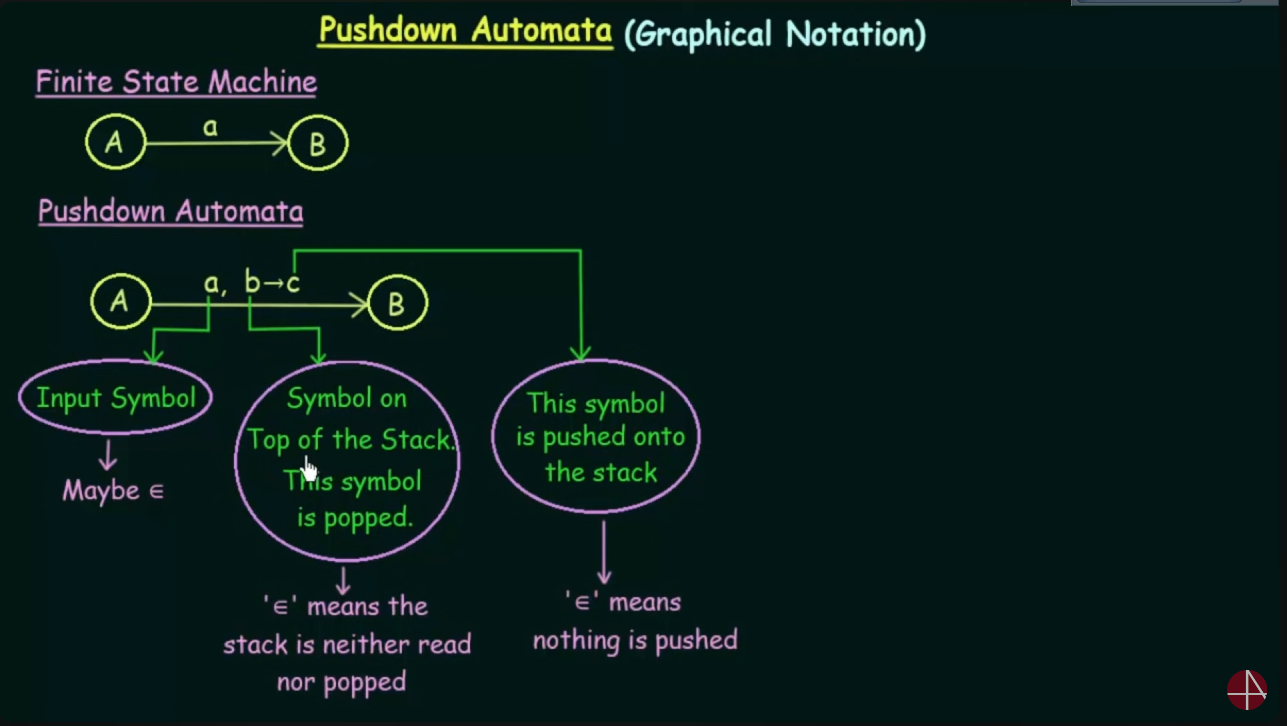

This one right here is non-deterministic pushdown automata.
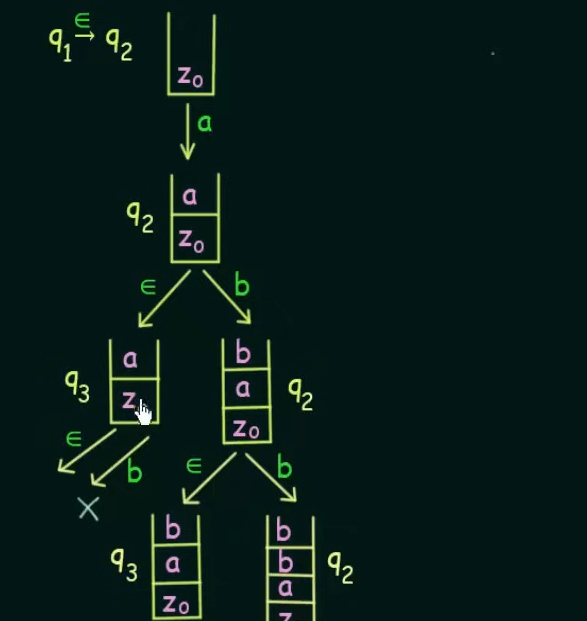
Pushdown Automata -- Even Palindromes
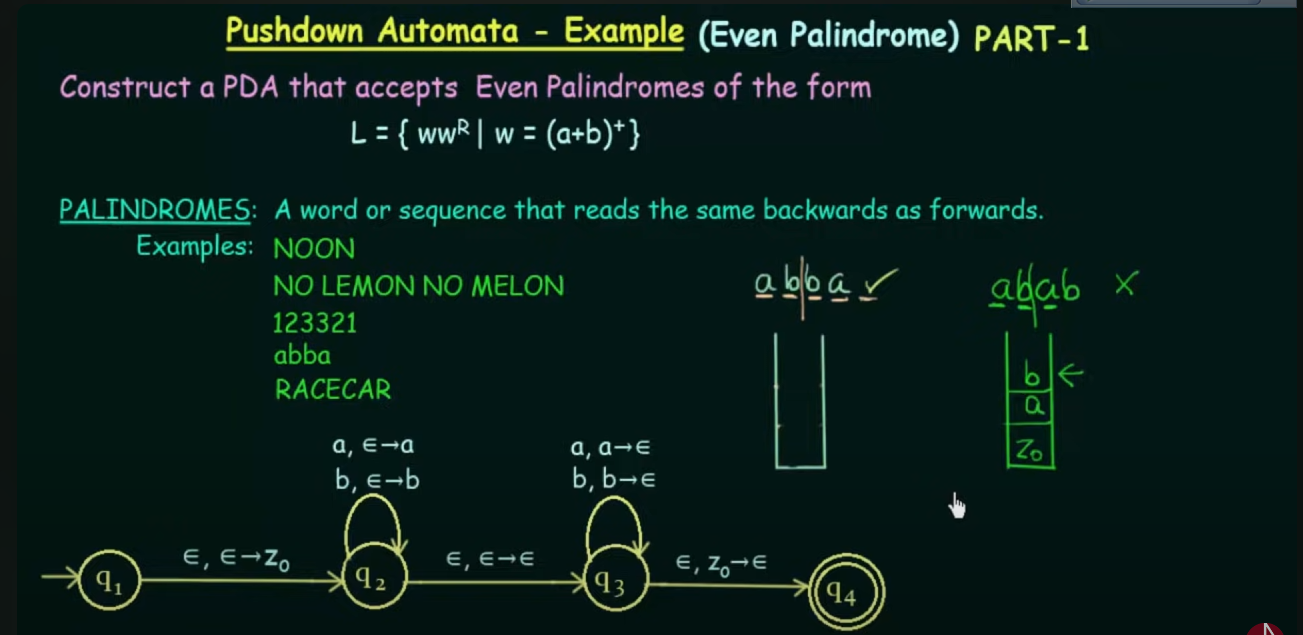
Here we have designed non-deterministic PDA in which it's a bit hard to figure out, when we have reached the middle of the string.
So we introduce epsilon between every string. https://www.youtube.com/watch?v=BxA-aI2dyRo&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=89

This results in a huge tree of possible inputs