Regular Languages and Finite Automata -- Formal Language and Automata Theory -- Module 1 and Module 2

#Semester-4

Index

Basic Terminologies
Chomsky Hierarchy of languages
Deterministic Finite Automata (DFA)
Non-deterministic Finite Automata
Finite Automata with outputs.
Conversion of NFA to DFA
Regular Expressions
Identities of Regular expressions
Conversion of NFA to Regular Expression
Conversion of Regular expression to Finite Automata
Pumping Lemma for Regular Languages.
Regular Grammar
Derivations from a Grammar

Basic Terminologies

Symbol : Any alphanumeric stuff : "a, b, c, 0, 1, 2, 3".... and so on.
Alphabet : $\sum$ , denotes a collection of symbols. For example $\sum - > {a, b}$ or $\sum - > {d, e, f, g}$ or $\sum - > {0, 1, 2}$
String : "A sequence of symbols". For example: "a,b,0,1,aa,bb,ab,01"
Language: A set of strings. For example $\sum - > {0, 1}$

Let L1 be a set of strings of length 2

Therefore $\sum - > {00, 01, 10, 11}$

L2 = Set of strings of length 3

$\sum - > {000, 001, 010, 011, 100, 101, 110, 111}$

This can also be expressed as powers of $\sum$ .

For first case, it will be L1 = $\sum^{2}$

For second case, it will be L2 = $\sum^{3}$

Finite Automata

There's two types of Finite Automata

Finite Automata without Output:
1. Deterministic Finite Automata (DFA)
2. Non-Deterministic Finite Automata (NFA)
Finite Automata with Output:
1. Moore Machine
2. Mealy Machine

Deterministic Finite Automata (DFA)

It is the simplest model of computation
It has a very limited memory.

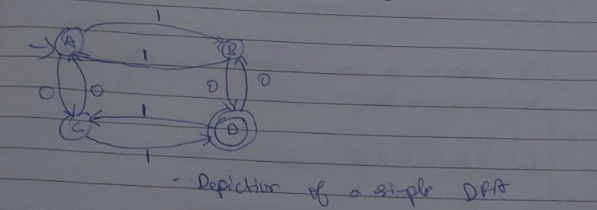
Pasted image 20240616123130.png

Here A,B,C,D are the states. The edges having "0" or "1" are the inputs and also the transition states which determine which state will the DFA shift to.

The incoming arrow at state A indicates that A is the starting state.

The double circle in state D indicates that it is the final state of the DFA.

Every DFA/NFA can be defined using these 5 tuples

(Q, $\sum$ , $q_{0}$ , F, $δ$ )

Pasted image 20240616124030.png
Symbol Pronunciation

$\sum$ = sigma (not the brainrot sigma kid)
$q_{0}$ = q "not"
$δ$ = delta

Example

Pasted image 20240616124403.png

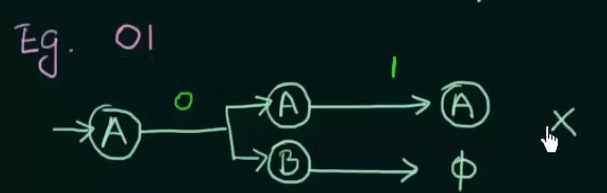
Start from initial state A. Since we can only have input strings which start with 0, we send it to a final state B. Now in case B receives any more inputs, those will be looped at B.

Now we need to take care of the case of input strings starting with 1. Therefore we design another state C where those strings are sent and subsequent inputs in C, stay at C.

This state C is also known as the "dead state" where unwanted strings go to in DFA.

Non-deterministic Finite Automata

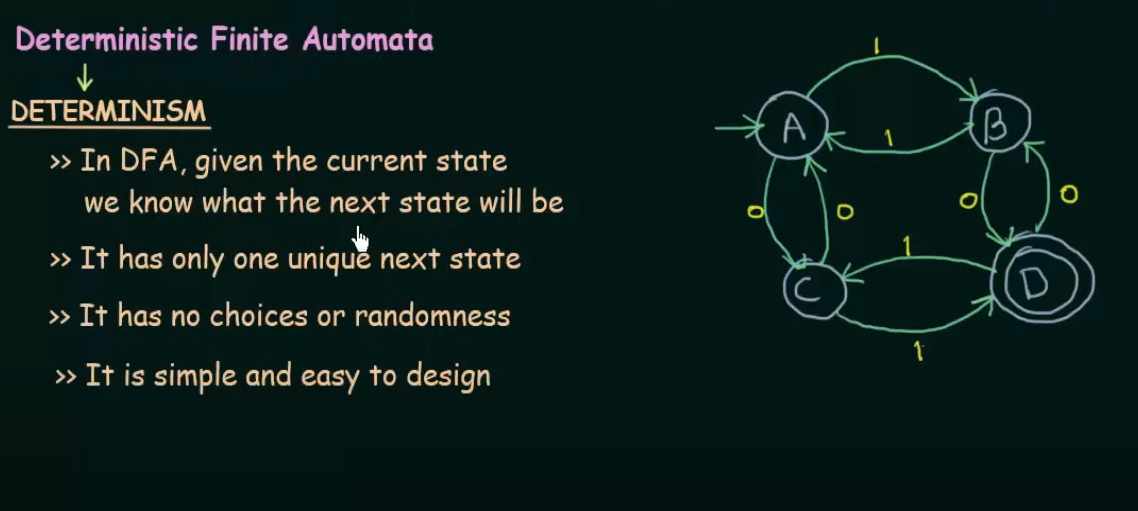
Pasted image 20240616125013.png

Pasted image 20240616125035.png

The main difference between DFA and NFA is that in DFA all the states are pre-determined and there is only one unique next state, however in NFA there could be, given the current state multiple next states and the next state may be chosen at random and all the next states could be chosen in parallel.

Pasted image 20240616125512.png

Here, instead of sending the input strings which start with 1 to a dead state C, it was looped into A itself.

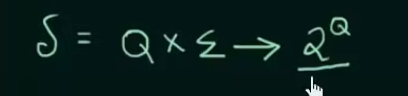
Pasted image 20240616125743.png

Examples

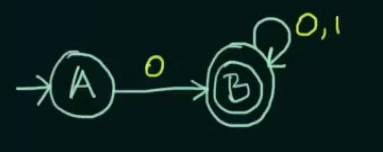
Let's test this using a test string "100"

Pasted image 20240616125913.png

and another test string "01"

Pasted image 20240616130056.png

Pasted image 20240616130106.png

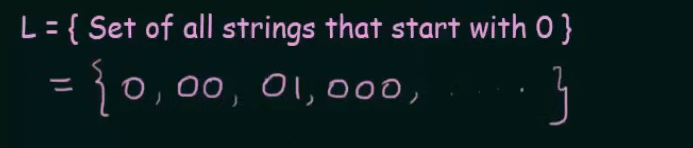
Let's create an NFA for this set

We start with our initial state A and another state B

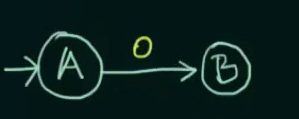
Pasted image 20240616130306.png

We declare B as final state and for any subsequent inputs to B, we loop them into B itself

Pasted image 20240616130356.png

Now we could have looped inputs of 1 into A itself, or sent it to a final state in case of a DFA, but in this case of an NFA, this NFA is complete.

Example test strings

Pasted image 20240616130536.png

So we need to make two states whose combined inputs will result in a string of length 2 and a final state to hold the strings.

Pasted image 20240616130733.png

Note that we want our NFA to be restricted to the values of set L and thus we didn't make any changes to final state C.

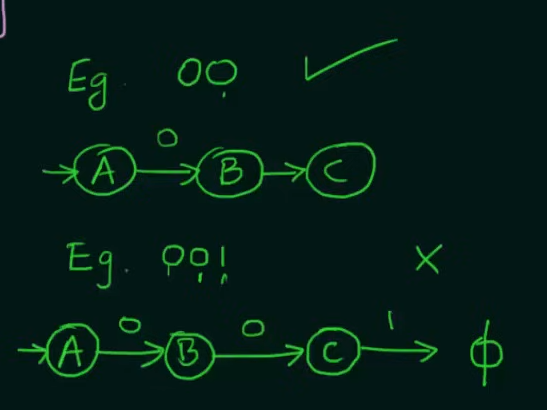
Pasted image 20240616130842.png

All example videos on NFA:

https://www.youtube.com/watch?v=4bjqVsoy6bA&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=12
https://www.youtube.com/watch?v=Bcen1W_uFEU&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=13
https://www.youtube.com/watch?v=--CSVsFIDng&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=15

Conversion of NFA to DFA

Pasted image 20240616131058.png

Example.

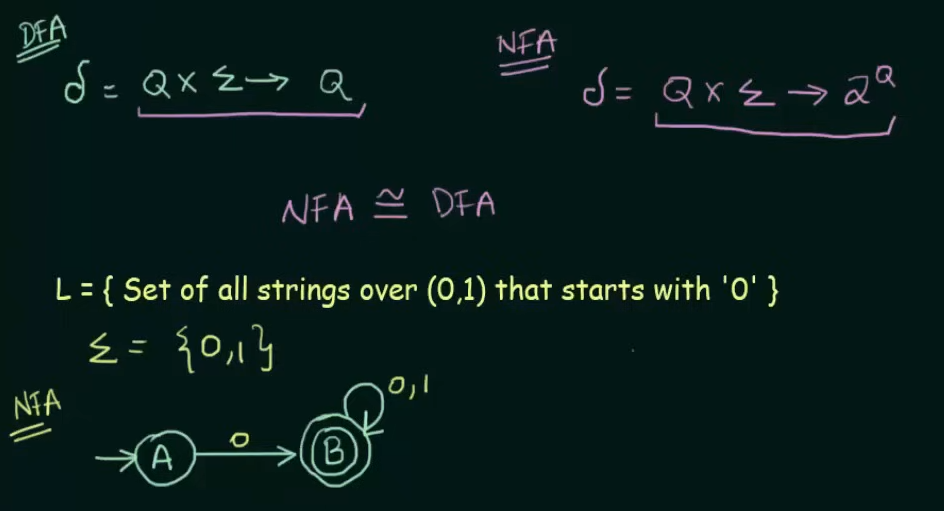
Pasted image 20240616131146.png

Given NFA here.

Step 1. Make the state transition table for the NFA.

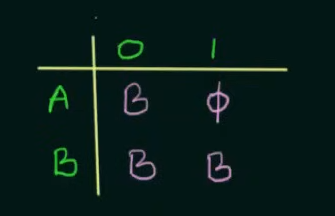
Pasted image 20240616131214.png

Here as we can see, on input 0, A goes to B and on input 1, A goes to $ϕ$ (NULL)
On input 0, B loops back to itself and on getting input 1, B goes to $ϕ$ (NULL)

Step 2. Make the state transition table for the resultant DFA from the state transition table of the NFA.

Pasted image 20240616131500.png

Since we cannot leave unwanted strings to loop in any other state than a dead state in DFA, we put a new state C in place of $ϕ$ .

And since we created a new state C, we need to define the transitions on C as well, which loops to itself despite any input to state C.

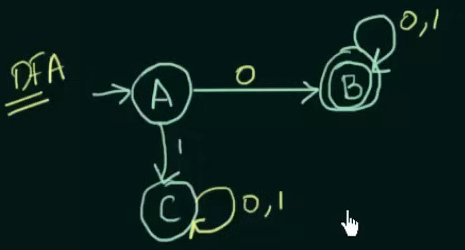
Pasted image 20240616131655.png

Thus the new resultant DFA.

Example 2. (Important)

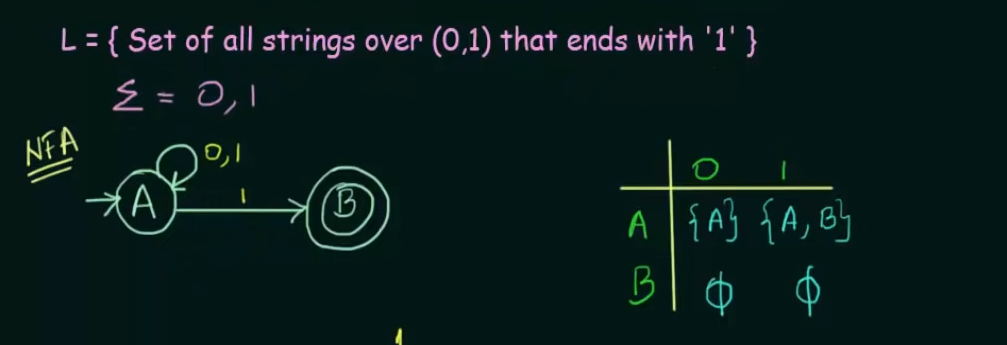
Pasted image 20240616132628.png

Here's our given NFA and it's transition state table. Note that on an input of 1, state A loops to itself and also goes to final state B, to represent that we created a new state which represents states ${A, B}$ .

In case of a DFA since there is only one unique next state we need to represent ${A, B}$ using a new state AB.

And we also need to define the state transitions of AB.

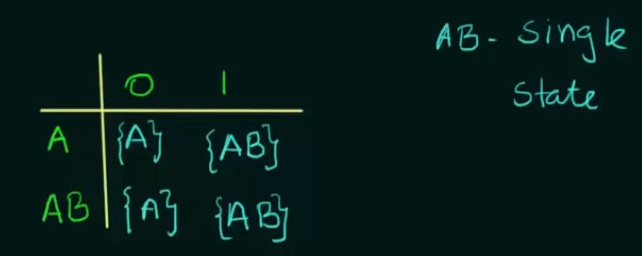
Pasted image 20240616133149.png

This method of creating new states which contains more than one state is called "Subset creation method".

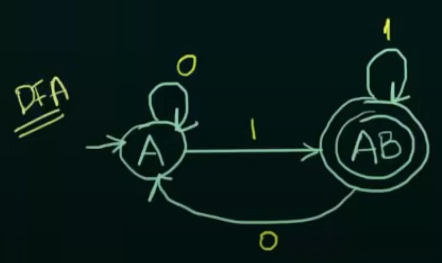
Thus the resultant DFA will be:

Pasted image 20240616133304.png

Minimization of DFA

Minimization of DFA is required to obtain the minimal version of any DFA which consists of the minimum number of states possible.

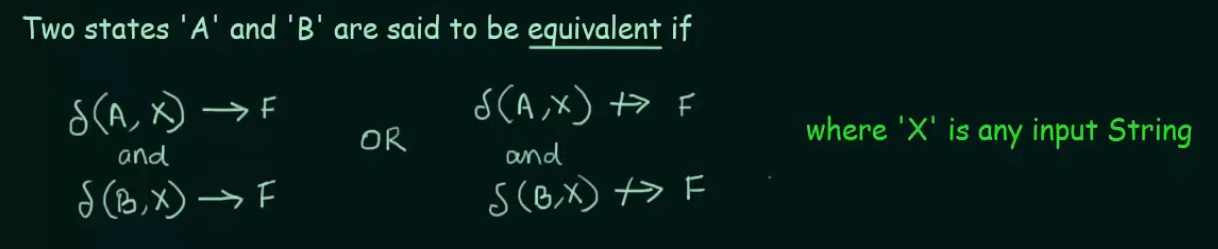
Pasted image 20240616133741.png

Pasted image 20240616133754.png

Let's understand this practically using examples.

Example 1.

Given a DFA and it's state transition table.

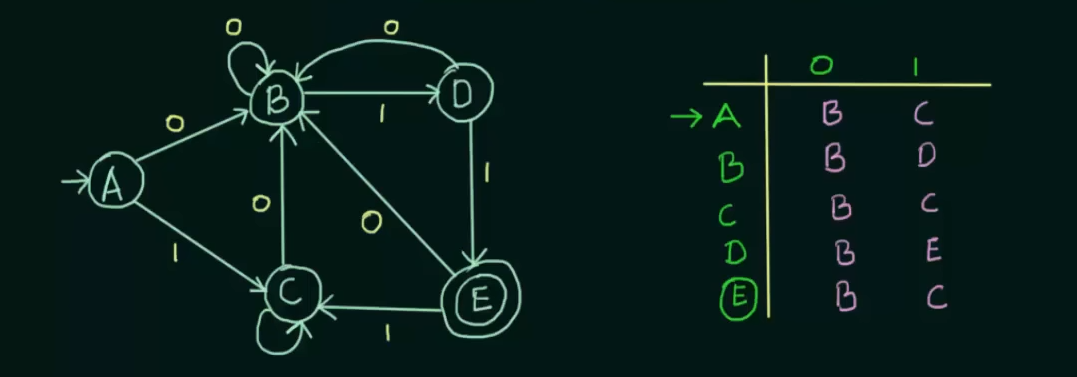
Pasted image 20240616133947.png

Step 1. Write the zero equivalence as two separate sets : {Set of non-final states}

0 equivalence = ${A, B, C, D}$ ${E}$

Step 2. Write 1 equivalence.

Here we see that in the first set, there are 4 states. Now we need to see if those states are 1 equivalent to each other. How we do that is we take pairs of the sets, then check if the next states of the pairs are equal to each other . If so then the pair is 1 equivalent to each other.

We get to see that for input 0, both A and B go to state B and for input 1, we see that A goes to state C and B goes to state D.

Thus we need to check if C and D are 1 equivalent to each other or not.

We see that both C and D go to state B on input 0 and on input 1, C loops to itself and D goes to state E.

Now we also see that A and C share the same next states for both inputs.

Thus C and D are not 1-equivalent to each other.

Therefore

1 equivalence = ${A, B, C}$ ${D}$ ${E}$

Step 3: Check for 2-equivalence using the same method

Use the row of 1-equivalence

We will only focus on the set of ${A, B, C}$

We know that on input 0, A and B go to the same states, but on input 1, A goes to state C and B goes to state D.

Check if C and D are in the same set or not. [False].
Thus A and B are not 2-equivalent to each other.

Thus,

2 equivalence = ${A, B}$ ${C}$ ${D}$ ${E}$

Now we see that for any further equivalences, the result is the same, so we can stop the process here.

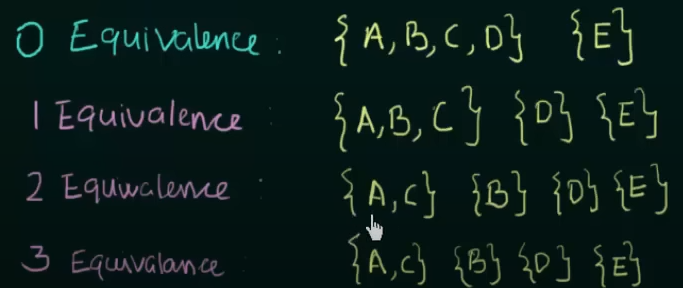
Pasted image 20240616150754.png

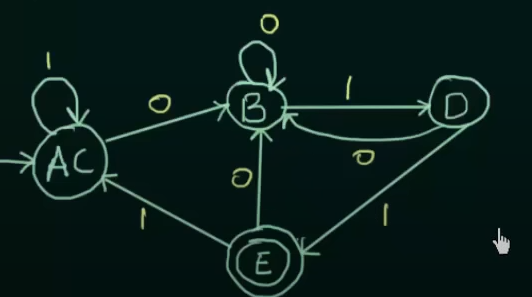
Now using this equivalence and the existing transition state table, we get the new minimized DFA

Pasted image 20240616151009.png

Where AC is treated as a single new state.

Therefore, DFA before minimization

Pasted image 20240616150927.png

And DFA after minimization

Pasted image 20240616150957.png

More examples on the DFA minimization

https://www.youtube.com/watch?v=0XaGAkY09Wc&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=21
https://www.youtube.com/watch?v=ex9sPLq5CRg&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=22
https://www.youtube.com/watch?v=DV8cZp-2VmM&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=23
https://www.youtube.com/watch?v=kYMqDgB2GbU&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=24

Finite Automata with outputs.

Till now the automata we dealt with produced no outputs.

Now we will be dealing with automata with outputs.

Pasted image 20240616151234.png

Don't focus on the symbol descriptions too much, it's just filler theory.

Example

Pasted image 20240616151426.png

The main difference between Mealy Machine and Moore Machine is that

Mealy Machines produce outputs during the transition phase (When A goes to A or B or wherever)

Moore Machines produce outputs within the state itself (When A or B or any other state is reached)

Construction of Mealy Machine

Pasted image 20240616151704.png

Now we know that outputs in Mealy machines are produced during the transition phase.

There for any strings like this :

Pasted image 20240616151754.png

will result in a Mealy Machine like this :

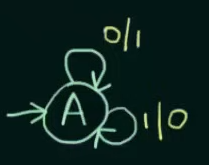
Pasted image 20240616151813.png

The format of "0/1" is : input/output, saying that the first half indicates the input of the state and the second indicates the output.

Pasted image 20240616151936.png

Here $\sum$ = the set of inputs and $Δ$ = the set of outputs

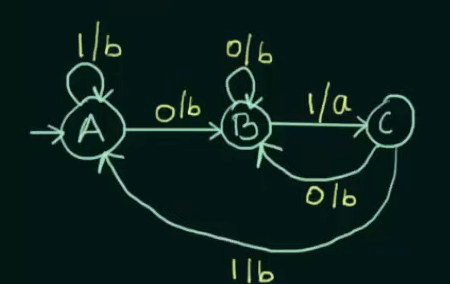
Pasted image 20240616152239.png

This will be resultant Mealy Machine.

Here since we want the sequence "01" only, hence we send the input of 0 from C to B and the input of 1 from C to A.

And the transition phase from B to C of 1, resulting in the total sequence of "01", will output the string a, the rest of the inputs will output the string b, but are looped into themselves or sent to other states.

Example

Pasted image 20240616153247.png

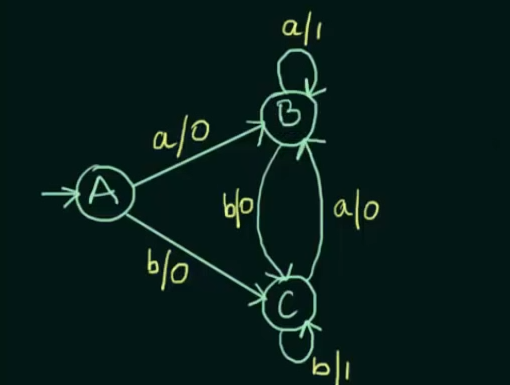
Pasted image 20240616153325.png

This will be the resulting Mealy Machine

More examples

https://www.youtube.com/watch?v=s-Ul9dIS9AE&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=29
https://www.youtube.com/watch?v=fkdufhcBraw&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=30

Construction of Moore Machine

Pasted image 20240616193153.png

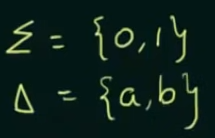
Pasted image 20240616193215.png

Step 1. Construct a DFA for a binary string that will end with 01.

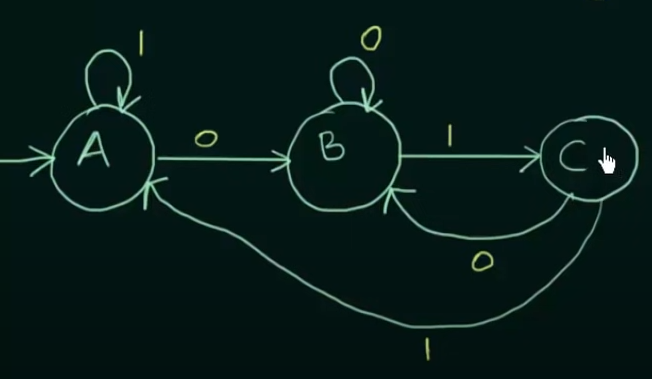
Pasted image 20240616193827.png

Now just add the outputs to the states

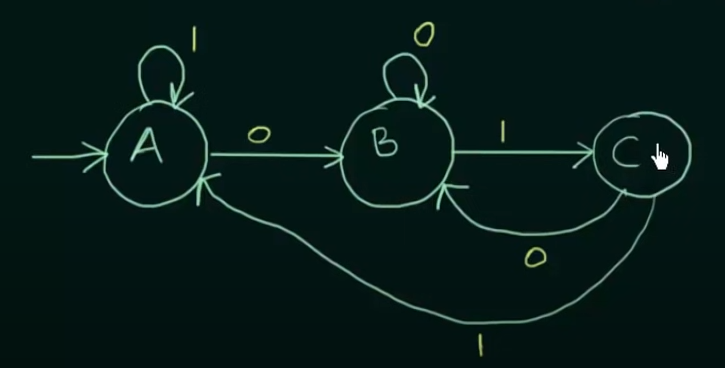
Pasted image 20240616193846.png

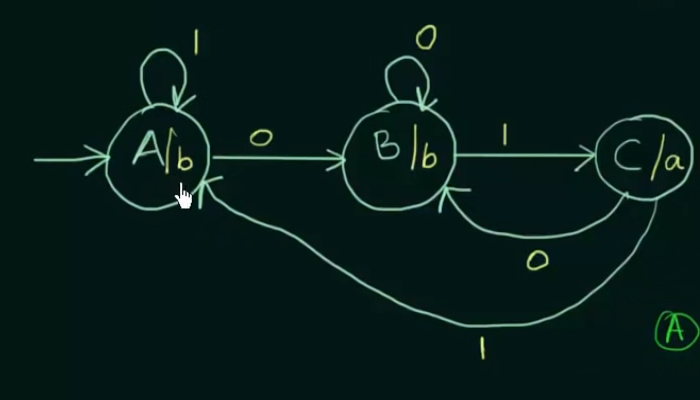
Pasted image 20240617204412.png

Conversion of Moore to Mealy machine

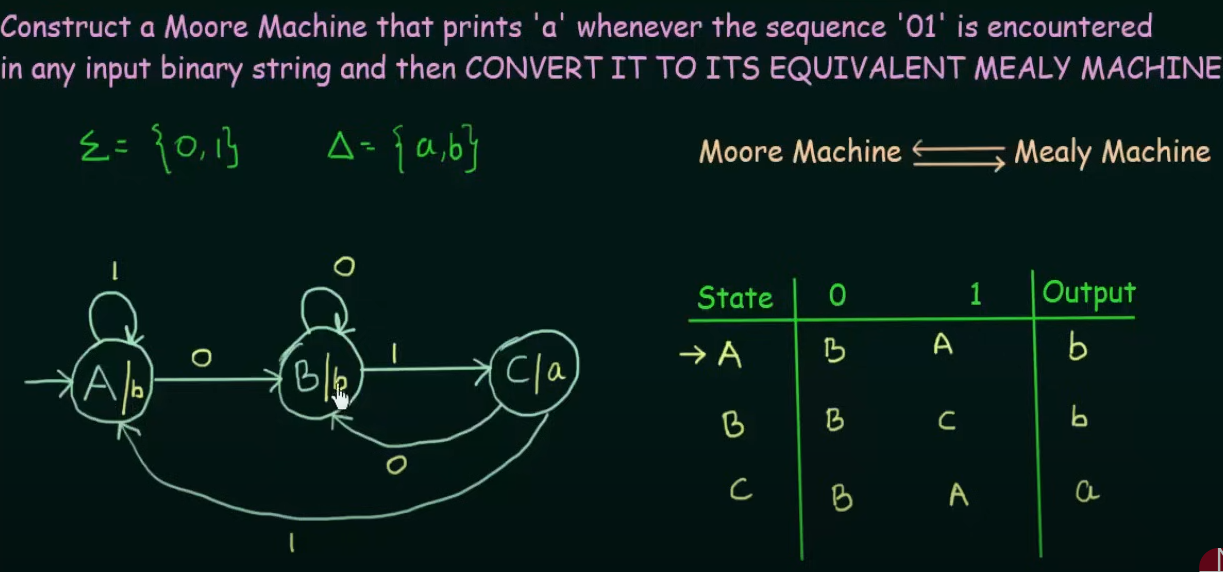
Pasted image 20240616195031.png

Here, we have been given a Moore Machine.

To convert to a Mealy machine, we have to put the same output of the state to it's incoming edge.

Therefore the resulting Mealy Machine will be :

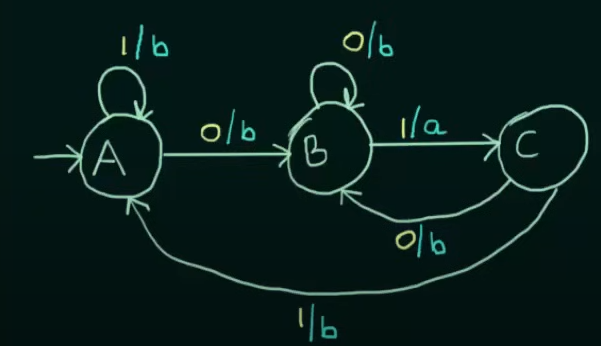
Pasted image 20240616195246.png

And we need to change the state transition table accordingly by writing the outputs besides the states and removing the output column :

Pasted image 20240616195344.png

Conversion of Mealy Machine to Moore Machine

Pasted image 20240616195453.png

Thus set of inputs , $\sum$ = {a, b} and set of outputs $Δ$ =

Now since states B and C output two different values, they will be separated into states $B_{1}$ and $C_{1}$ .

And the output on the states will be the same the outputs on the edges incoming to them.

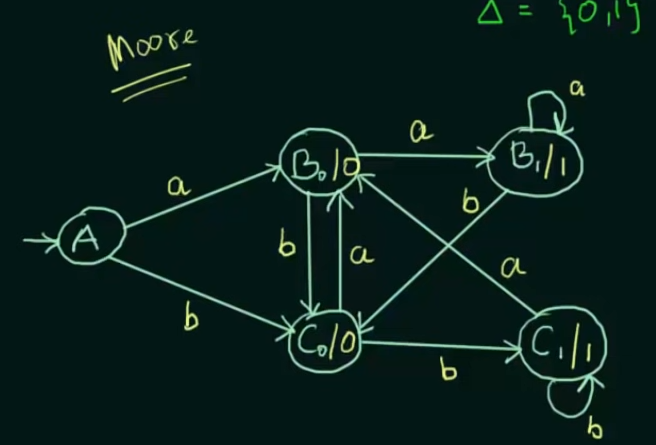
Pasted image 20240616195841.png

Now state A didn't have to be separated since there are no incoming outputs on A.

Another example video :

https://www.youtube.com/watch?v=t48LqMDqNrA&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=39

Regular Languages

Pasted image 20240616200035.png

Regular Expressions

Pasted image 20240616200124.png

Pasted image 20240616200204.png

Important operations to remember in Regular Expressions.

Union : The union of any two RE is denoted by $R_{1} + R_{2}$
Concatenation : The concatenation of any two RE is denoted by $R_{1} . R_{2}$
Iteration/Closure: The iteration of any RE is denoted by $R E^{*}$ .
For example :

$a^{*}$ = { ^, a, aa, aaaa}.... where ^ is called the empty symbol. The empty symbol's presence is mandatory for such an RE to be considered a closure.

Examples

Pasted image 20240616200728.png

Any comma in the set is denoted by Union (or), but if it has the empty symbol as in example 2, it is denoted by concatenation(and).

Identities of Regular expressions

Pasted image 20240616200856.png

https://www.youtube.com/watch?v=yp4pYgXfYD8&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=47

Arden's Theorem

Pasted image 20240616201124.png

Proof in case someone wants to memorize this

Pasted image 20240616201148.png

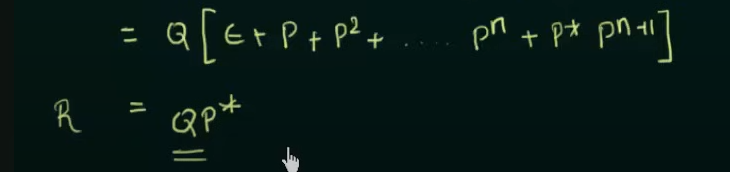
Pasted image 20240616201208.png

https://www.youtube.com/watch?v=Idl_0mPzZjE&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=48

Example video

https://www.youtube.com/watch?v=TkqcPh0BFUw&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=49

Designing of Regular Expressions

Pasted image 20240616213938.png

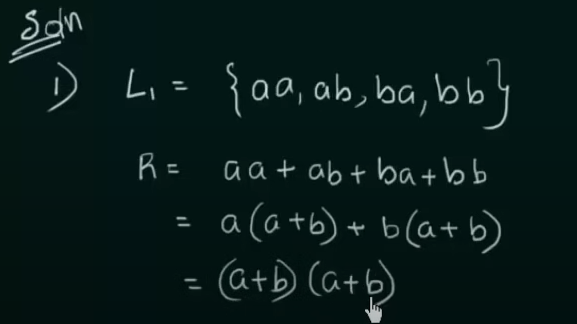
Pasted image 20240616213947.png

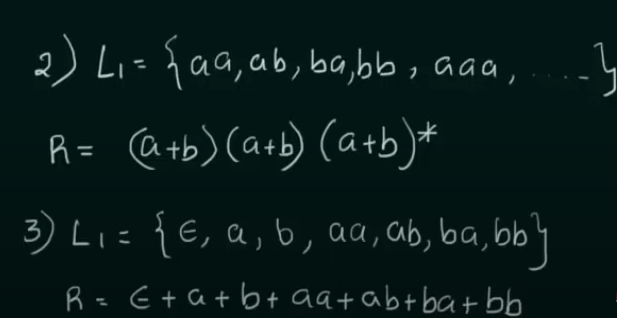
Pasted image 20240616214027.png

https://www.youtube.com/watch?v=FOhEmW_nMRs&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=50

Conversion of NFA to Regular Expression

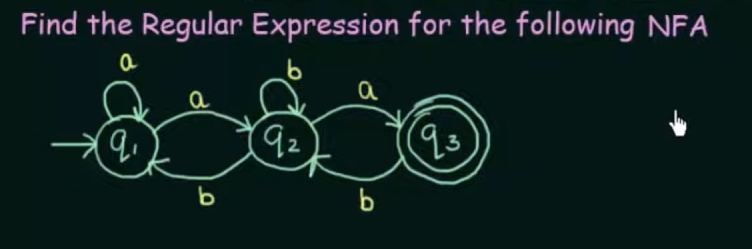
Pasted image 20240617005857.png

Step 1. Create equations of each state which includes it's incoming state transitions

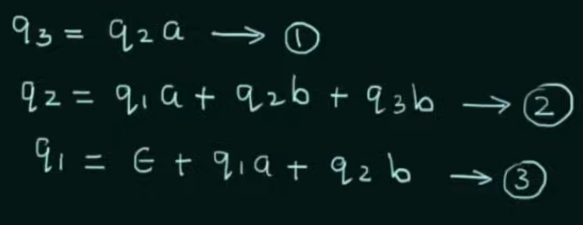
Pasted image 20240617010003.png

Solve the equations to get an RE in terms of the final state.

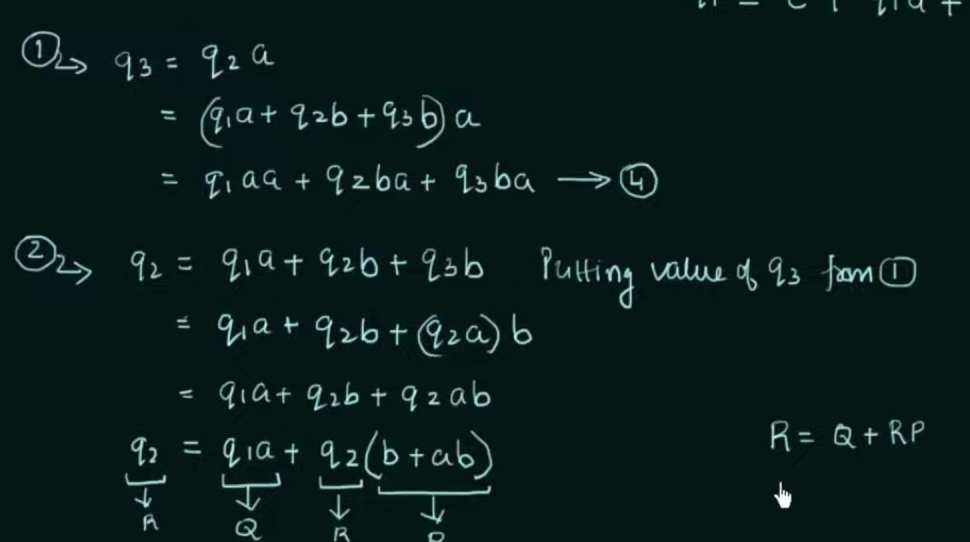
Pasted image 20240617010225.png

Thus, by Arden's Theorem:

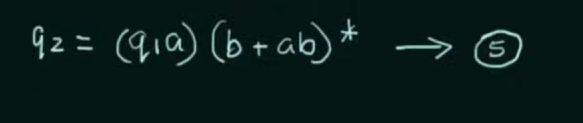
Pasted image 20240617010302.png

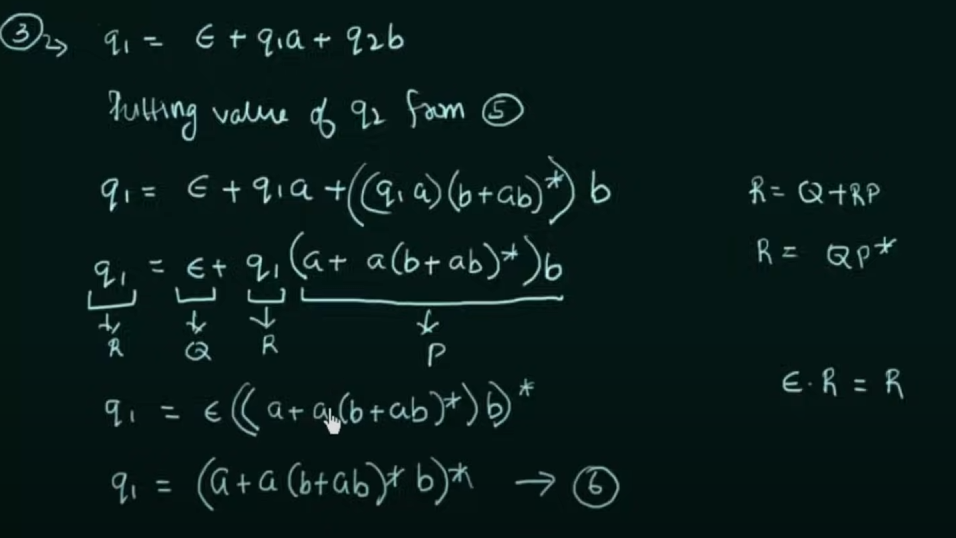
Pasted image 20240617010327.png

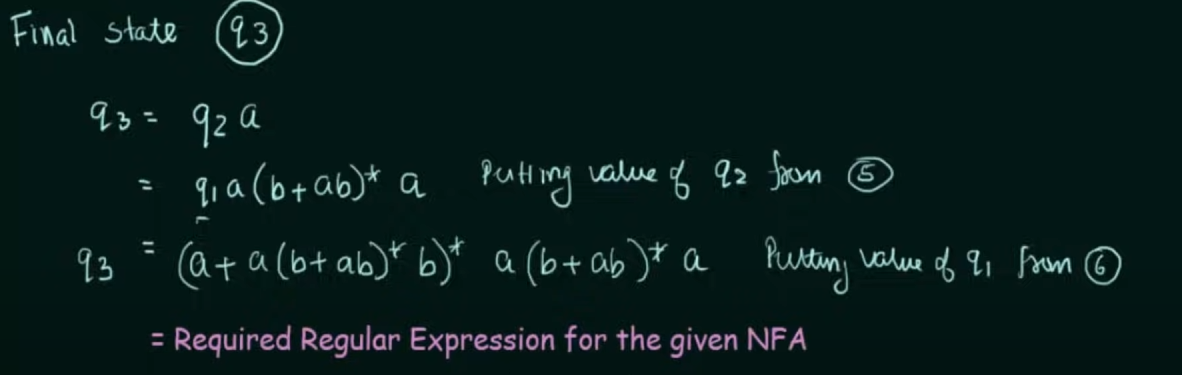
Pasted image 20240617010346.png

Conversion of DFA to Regular Expression

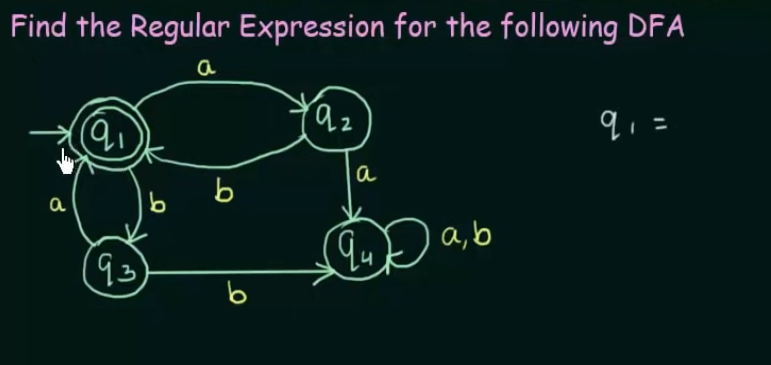
Pasted image 20240617010552.png

Pasted image 20240617010607.png

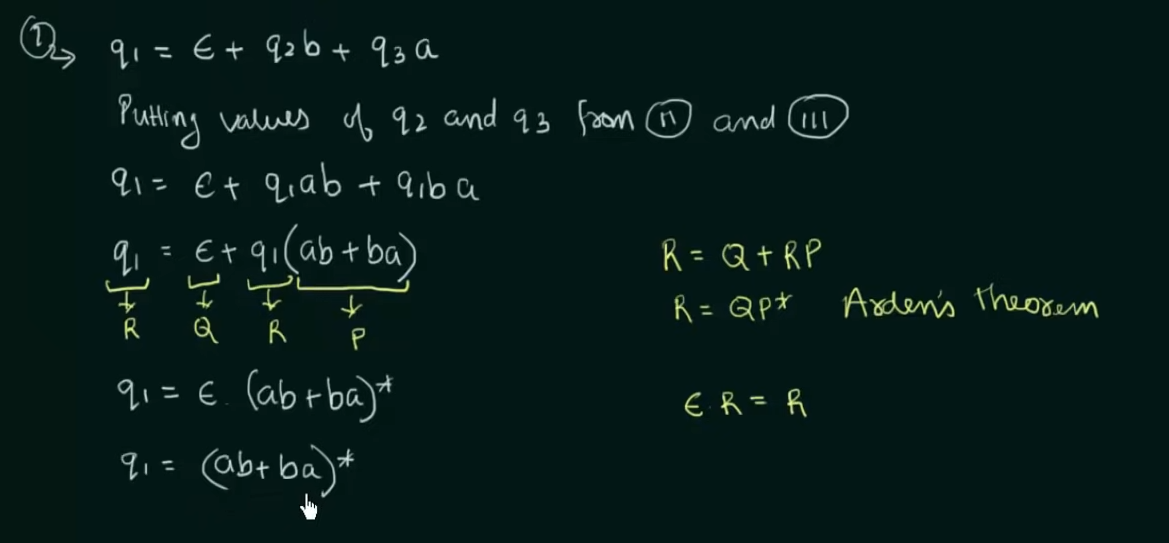
Pasted image 20240617010629.png

Example 2: When DFA has multiple final states

Pasted image 20240617010720.png

Find RE in terms of both the final states then perform a Union of the two

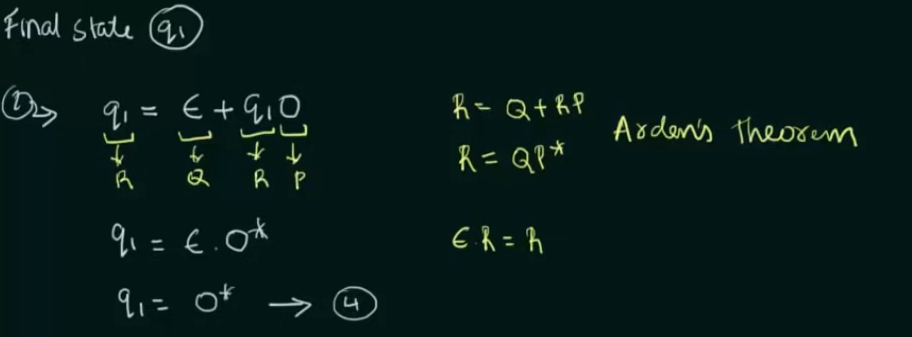
Pasted image 20240617010751.png

Pasted image 20240617010813.png

Conversion of Regular expression to Finite Automata

Pasted image 20240617075911.png

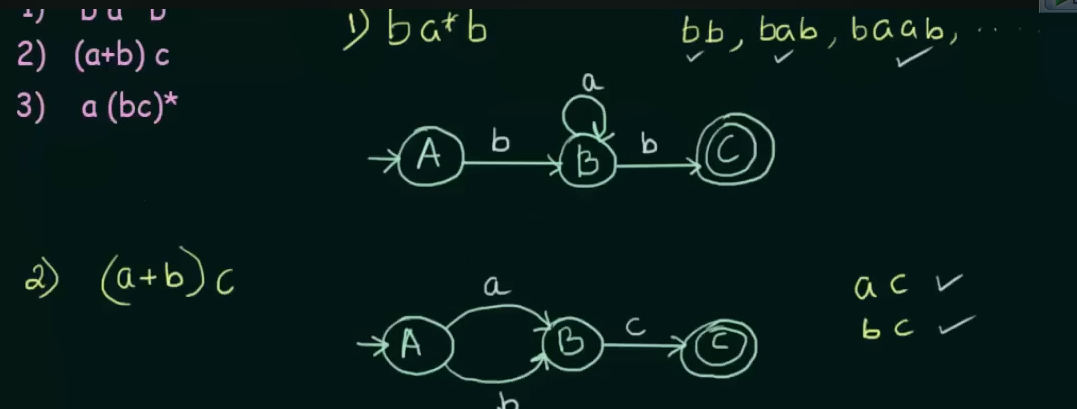
Union : both inputs can go to the same state.
Concatenation: Will need two states of one input each
Closure: Will loop into that state itself.

Example

Pasted image 20240617080530.png

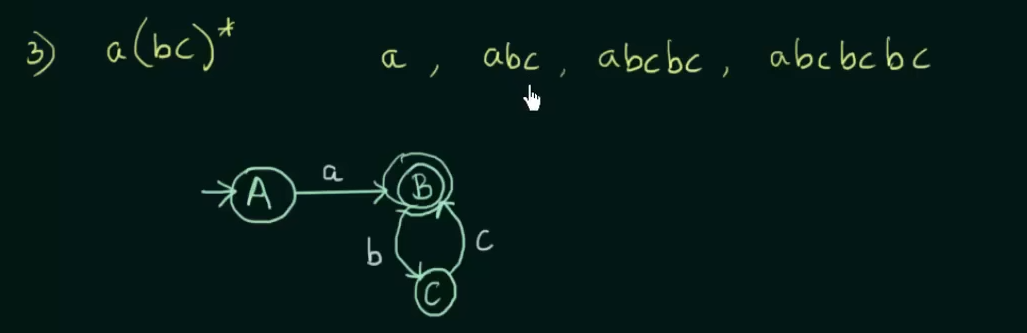
Pasted image 20240617080547.png

Pasted image 20240617080831.png

All example videos on this topic :

https://www.youtube.com/watch?v=62JAy4oH6lU&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=55
https://www.youtube.com/watch?v=RsSQPwUIR8U&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=56
https://www.youtube.com/watch?v=zSHS_7omxRY&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=57

Equivalence of two finite automata

Pasted image 20240617081007.png

Basically what we need to do is to see that for any pair of states, the pair of states both should either be intermediate states or final states.

And if If the initial state of one automata is a final state, it should be the same for the other automata.

Pasted image 20240617081803.png

Here FS stands for Final State and IS stands for intermediate state.

Example

Pasted image 20240617081915.png

Here we can see that the second point is already satisified.

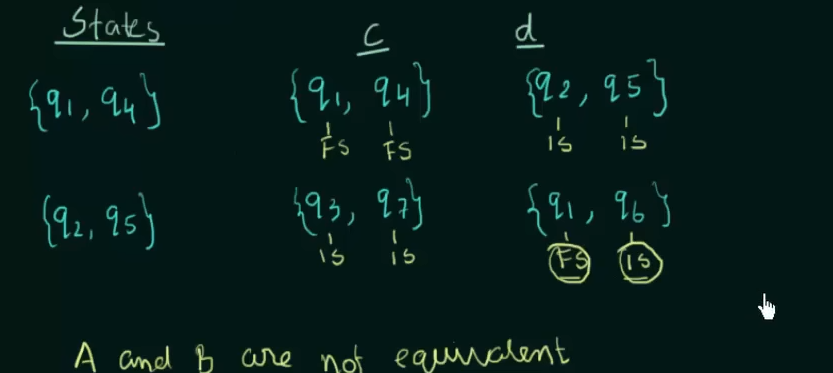
Pasted image 20240617082126.png

Here we could see that on input d, state q2 went to state q1 which is a final state and state q5 went to state q6 which is a intermediate state. This goes against the rule that for any two automata, any selected pair of states should be of the same kind.

Thus the automata A and B are not equivalent.

Pumping Lemma for Regular Languages.

Pasted image 20240617082405.png

** Pasted image 20240617082427.png

Example

https://www.youtube.com/watch?v=Ty9tpikilAo&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=61

Pasted image 20240617082528.png

Let us assume that A is regular

Then it must have some pumping length P

Let P = 7

Therefore A = $a^{7} b^{7}$ (we can also take the string variable as S, but A is preferred to maintain consistency)

Now we can break down A (or S) into three parts such that $S = x y z$

Therefore let S = aaaaaaaabbbbbbb (contains 7 a and 7 b)

Since this entire string can be broken down into three parts $x y z$ , we can check for the satisfiability of the first condition

$x y^{i} z \in A \forall i \geq 0$

Thus we get three cases

Pasted image 20240617083112.png

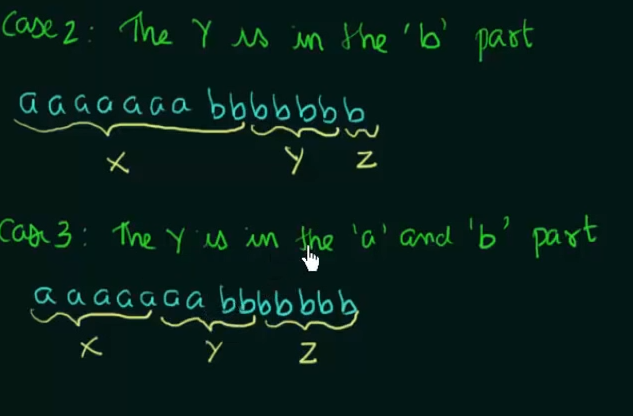
Pasted image 20240617083152.png

Now we need to show that none of the three conditions can be satisfied at the same time (could be none at all, or 2 satisfied 1 unsatisfied or 1 unsatisfied 2 satisfied but not 3 satisfied at the same time).

So, for the first condition, let i = 2.

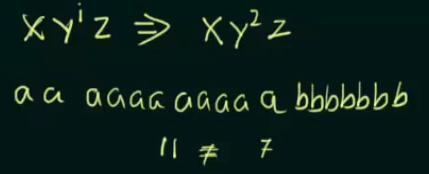
Pasted image 20240617083405.png

so, according to case 1, and the value of i, we need to write the part of y twice.

and we find that the total number of strings is greater than that of the pumping length P.

Thus case 1 does not satisfy the first condition.

Similarly :

Pasted image 20240617083622.png

Since the first condition itself couldn't be satisfied, we don't need to check the remaining two conditions.
Hence, the language $A = {a^{n} b^{n} | n \geq 0}$ is NOT regular.